题目内容
设直线系M：xcosθ+（y-2）sinθ=1（0≤θ≤2π），对于下列四个命题：（1）M中所有直线均经过一个定点；
（2）存在定点P不在M中的任一条直线上；
（3）对于任意正整数n（n≥3），存在正n边形，其所有边均在M中的直线上；
（4）M中的直线所能围成的正三角形面积都相等．
其中真命题的序号是
分析：先弄清直线系M中直线的特征，直线系M表示圆 x2+（y-2）2=1 的切线的集合，再判断各个结论的正确性．
解答：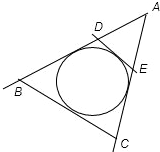
解：由 直线系M：xcosθ+（y-2）sinθ=1（0≤θ≤2π），可令
，
消去θ可得 x2+（y-2）2=1，故 直线系M表示圆 x2+（y-2）2=1 的切线的集合，
故（1）不正确．
因为对任意θ，存在定点（0，2）不在直线系M中的任意一条上，故（2）正确．
由于圆 x2+（y-2）2=1 的外且正n 边形，所有的边都在直线系M中，故（3）正确．
M中的直线所能围成的正三角形的边长不一等，故它们的面积不一定相等，
如图中等边三角形ABC和 ADE面积不相等，
故（4）不正确．
综上，正确的命题是 （2）、（3），故答案为 （2）、（3）．
解：由 直线系M：xcosθ+（y-2）sinθ=1（0≤θ≤2π），可令
|
消去θ可得 x2+（y-2）2=1，故 直线系M表示圆 x2+（y-2）2=1 的切线的集合，
故（1）不正确．
因为对任意θ，存在定点（0，2）不在直线系M中的任意一条上，故（2）正确．
由于圆 x2+（y-2）2=1 的外且正n 边形，所有的边都在直线系M中，故（3）正确．
M中的直线所能围成的正三角形的边长不一等，故它们的面积不一定相等，
如图中等边三角形ABC和 ADE面积不相等，
故（4）不正确．
综上，正确的命题是 （2）、（3），故答案为 （2）、（3）．
点评：本题考查直线系方程的应用，要明确直线系M中直线的性质，依据直线系M表示圆 x2+（y-2）2=1 的切线的集合，结合图形，判断各个命题的正确性．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目