��Ŀ����
��֪ԲMx2+y2-2tx-6t-10=0����ԲC��
+
=1��a��b��0��������ԲC��x��Ľ���A��5��y0���������ߵľ���Ϊ
����A��ԲM�⣬��ԲM�ϵĵ�͵�A������������С����֮��Ϊ2��
��1����ԲM�ķ��̺���ԲC�ķ��̣�
��2�����PΪ��ԲC������һ�㣬�Ե�P��ԲM�����ߣ��е�ֱ�ΪA��B��������ȥ��
A•
B��ȡֵ��Χ��
��3����ֱ��ϵM��xcos��+��y-3��sin��=1���ȡ�R������֤��ֱ��ϵM�е�����һ��ֱ��l���붨Բ���У���ֱ��д�����߶���ֱ��ϵM�е�ֱ���ϵ����п��ܵĵ���ֱ�������ε������
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 3 |
��1����ԲM�ķ��̺���ԲC�ķ��̣�
��2�����PΪ��ԲC������һ�㣬�Ե�P��ԲM�����ߣ��е�ֱ�ΪA��B��������ȥ��
| P |
| P |
��3����ֱ��ϵM��xcos��+��y-3��sin��=1���ȡ�R������֤��ֱ��ϵM�е�����һ��ֱ��l���붨Բ���У���ֱ��д�����߶���ֱ��ϵM�е�ֱ���ϵ����п��ܵĵ���ֱ�������ε������
��������1��������õ�a=5����A����Բ���ߵľ������
�õ�c��ֵ����b2=a2-c2���b2������Բ���̿�������ԲM�ϵĵ�͵�A������������С����֮��Ϊ2����Բ�İ뾶����1���t��ֵ����Բ�ķ��̿���
��2����ΪԲM��Բ������Բ�����ϣ�����Բ�ϵĵ��У������������ĵ����㣬������Զ�ĵ����Ҷ��㣬̽������P��λ����ʱ
A•
B��ֵ��С��P��λ����Բ�Ҷ���ʱ
A•
B��ֵ���
��3���ɵ㵽ֱ�߾��빫ʽ��֪���㣨0��3����ֱ��xcos��+��y-3��sin��=1���ȡ�R���ľ������1���ɴ�˵��ֱ��ϵM�е�����һ��ֱ��l���붨Բx2+��y-3��2=1���У���ͼ�������ܹ����ɵ���ֱ�������ε��������ͣ�����ƽ�漸��֪ʶ���ÿһ�ֵ���ֱ�������ε��������������
| 10 |
| 3 |
��2����ΪԲM��Բ������Բ�����ϣ�����Բ�ϵĵ��У������������ĵ����㣬������Զ�ĵ����Ҷ��㣬̽������P��λ����ʱ
| P |
| P |
| P |
| P |
��3���ɵ㵽ֱ�߾��빫ʽ��֪���㣨0��3����ֱ��xcos��+��y-3��sin��=1���ȡ�R���ľ������1���ɴ�˵��ֱ��ϵM�е�����һ��ֱ��l���붨Բx2+��y-3��2=1���У���ͼ�������ܹ����ɵ���ֱ�������ε��������ͣ�����ƽ�漸��֪ʶ���ÿһ�ֵ���ֱ�������ε��������������
�����1���⣺�������֪a=5����
-a=
����a=5������c=3������b2=a2-c2=16��
������ԲC�ķ���Ϊ
+
=1��
��x2+y2-2tx-6t-10=0���ã�x-t��2+y2=t2+6t+10�����Ը�Բ��Բ����x���ϣ�
���A��ԲM�⣬��ԲM�ϵĵ�͵�A������������С����֮��Ϊ2����Բ�İ뾶����1��
����t2+6t+10=1�����t=-3��
����ԲM�ķ���Ϊ��x+3��2+y2=1��
��2���⣺��ͼ��
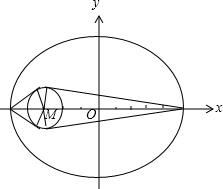
��ΪԲM��Բ��λ����Բ�����ϣ���Բ����Բ�ڲ���
������Բ���㵽ԲM��Բ�ľ�����������Pλ����Բ��ʱ|
|=|
|��С���ҡ�APB�����cos��
��
����С����Pλ����Բ�Ҷ���ʱ|
|=|
|����ҡ�APB��С����cos��
��
�����
��Pλ����Բ��ʱ����ͼ��֪�������߳�Ϊ
�������н�Ϊ60�㣬����ֵΪ
����Pλ����Բ�Ҷ���ʱ����ͼ��֪�������߳�Ϊ
�������н�һ�������ֵΪ
�������н�����ֵΪ1-2��(
)2=
��
����
A•
B����СֵΪ|
||
|COS60��=
��
��
=
�����ֵΪ
��
��
=
��
����
A•
B��ȡֵ��Χ��[
��
]��
��3��֤������Ϊxcos��+��y-3��sin��=1�����Ե�P��0��3����M��ÿ��ֱ�ߵľ���d=
=1��
��MΪԲC��x2+��y-3��2=1��ȫ��������ɵļ��ϣ�����ֱ��ϵM�е�����һ��ֱ��l���붨Բ
C��x2+��y-3��2=1����
���߶���ֱ��ϵM�е�ֱ���ϵ����п��ܵĵ���ֱ�������ε���������֣�һ����������������Բ������������
Բ���������ⲿ��
��ͼ��
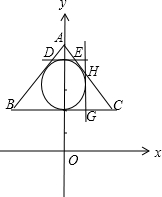
����ֱ��������ABC����AB=2+
�������S=
��(2+
)��(2+
)=3+2
��
����ֱ��������ADE����AD=2-
�������S=
��(2-
)��(2-
)=3-2
��
����ֱ��������GHC����GC=
�������S=
��
��
=1��
| a2 |
| c |
| 10 |
| 3 |
������ԲC�ķ���Ϊ
| x2 |
| 25 |
| y2 |
| 16 |
��x2+y2-2tx-6t-10=0���ã�x-t��2+y2=t2+6t+10�����Ը�Բ��Բ����x���ϣ�
���A��ԲM�⣬��ԲM�ϵĵ�͵�A������������С����֮��Ϊ2����Բ�İ뾶����1��
����t2+6t+10=1�����t=-3��
����ԲM�ķ���Ϊ��x+3��2+y2=1��
��2���⣺��ͼ��

��ΪԲM��Բ��λ����Բ�����ϣ���Բ����Բ�ڲ���
������Բ���㵽ԲM��Բ�ľ�����������Pλ����Բ��ʱ|
| PA |
| PB |
| PA |
| PB |
| PA |
| PB |
| PA |
| PB |
��Pλ����Բ��ʱ����ͼ��֪�������߳�Ϊ
| 3 |
| 1 |
| 2 |
| 63 |
| 1 |
| 8 |
| 1 |
| 8 |
| 31 |
| 32 |
����
| P |
| P |
| PA |
| PB |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 63 |
| 63 |
| 31 |
| 32 |
| 1953 |
| 32 |
����
| P |
| P |
| 3 |
| 2 |
| 1953 |
| 32 |
��3��֤������Ϊxcos��+��y-3��sin��=1�����Ե�P��0��3����M��ÿ��ֱ�ߵľ���d=
| 1 | ||
|
��MΪԲC��x2+��y-3��2=1��ȫ��������ɵļ��ϣ�����ֱ��ϵM�е�����һ��ֱ��l���붨Բ
C��x2+��y-3��2=1����
���߶���ֱ��ϵM�е�ֱ���ϵ����п��ܵĵ���ֱ�������ε���������֣�һ����������������Բ������������
Բ���������ⲿ��
��ͼ��

����ֱ��������ABC����AB=2+
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
����ֱ��������ADE����AD=2-
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
����ֱ��������GHC����GC=
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
���������⿼����Բ����Բ�ı����̣�������ƽ�����������������㣬������ֱ����Բ���ߵĹ�ϵ�����⿼����ѧ����̽��˼ά�����ͷ�ɢ˼ά�����������⣮

��ϰ��ϵ�д�
�����Ŀ