题目内容
为使关于x的不等式|x+1|+|x-2|≤a2+a+1(a∈R)的解集在R上为空集,则a的取值范围是( )
分析:|x+1|+|x-2|表示数轴上的x对应点到-1和2对应点的距离之和,其最小值等于3,由a2+a+1<3,解得x的取值范围.
解答:解:|x+1|+|x-2|表示数轴上的x对应点到-1和2对应点的距离之和,其最小值等于3,由题意关于x的不等式|x+1|+|x-2|≤a2+a+1(a∈R)的解集在R上为空集,可得,
a2+a+1<3,解得-2<a<0,
故选:B.
a2+a+1<3,解得-2<a<0,
故选:B.
点评:本题考查绝对值的意义,绝对值不等式的解法,得到a2+a+1<3,是解题的关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
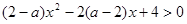 对一切实数x都成立,则a的范围是
;
对一切实数x都成立,则a的范围是
;