题目内容
（本题14分）已知椭圆的两个焦点
，且椭圆短轴的
两个端点与
构成正三角形．
（1）求椭圆的方程；
（2）过点（1，0）且与坐标轴不平行的直线
与椭圆交于不同两点P、Q，
若在
轴上存在定点E（
，0），使
恒为定值，求的值.
解：（1）由题意知 
=
又∵椭圆的短轴的两个端点与F构成正三角形
∴
=1 从而
∴椭圆的方程为
=1
（2）设直线
的斜率为
，则的方程为
消
得 
设
，则由韦达定理得
则
∴
=
=
=
=
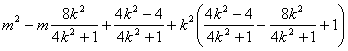
……………………………13
要使上式为定值须
， 解得 
故时，
为定值
练习册系列答案
科学实验活动册系列答案
相关题目
，焦点在
轴上，短轴长为2，且两个焦点和短轴的两个端点恰为一个正方形的顶点．过右焦点
与
交椭圆于
，
两点． 
的面积；
上是否存在点
,使得以
为邻边的平行四边形是菱形？
若存在，求出
的取值范围；若不存在，请说明理由.
的左、右焦点分别为F1、F2，其中
的焦点，M是C1与C2在第一象限的交点，且
上，求直线AC的方程。
，且椭圆短轴的两个端点与
构成正三角形．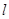
与椭圆交于不同两点P、Q，若在
轴上存在定点E（
，0），使
恒为定值，求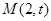
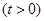在直线
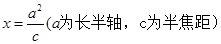上。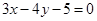
截得的弦长为2的圆的方程；