题目内容
(本题14分)已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点
轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点![]() 与
与![]() 轴不垂直的直线
轴不垂直的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)当直线![]() 的斜率为1时,求
的斜率为1时,求![]() 的面积;
的面积;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?
为邻边的平行四边形是菱形?
 若存在,求出
若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解析:
(Ⅰ)由已知,椭圆方程可设为![]() . ----------------1分
. ----------------1分
∵ 两个焦点和短轴的两个端点恰为正方形的顶点,且短轴长为2,
∴ ![]() .
.
所求椭圆方程为![]() . ---------------- 3分
. ---------------- 3分
(Ⅱ)右焦点![]() ,直线
,直线![]() 的方程为
的方程为![]() . ----------------4分
. ----------------4分
设![]() ,
,
由  得
得 ![]() ,解得
,解得 ![]() .-----------6分
.-----------6分
∴ ![]() . ----------------8分
. ----------------8分
(Ⅲ)假设在线段![]() 上存在点
上存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形.因为直线与
为邻边的平行四边形是菱形.因为直线与![]() 轴不垂直,所以设直线
轴不垂直,所以设直线![]() 的方程为
的方程为![]() . ----9分
. ----9分
由  可得
可得![]() .
.
∴![]() . -------10分
. -------10分
![]() .其中
.其中![]()
以![]() 为邻边的平行四边形是菱形
为邻边的平行四边形是菱形![]()
![]() ----12分
----12分
![]()
![]()
![]()
![]()
![]()
∴![]() . ----------------1 4分
. ----------------1 4分

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 ,且椭圆短轴的两个端点与
,且椭圆短轴的两个端点与 构成正三角形.
构成正三角形.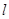 与椭圆交于不同两点P、Q,若在
与椭圆交于不同两点P、Q,若在 轴上存在定点E(
轴上存在定点E( ,0),使
,0),使 恒为定值,求
恒为定值,求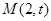
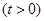 在直线
在直线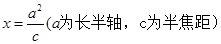 上。
上。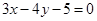 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;