题目内容
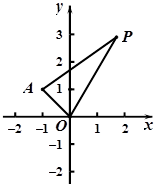
在平面直角坐标系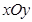 中,已知点
中,已知点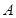
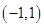 ,点P是动点,且三角形
,点P是动点,且三角形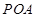 的三边所在直线
的三边所在直线
的斜率满足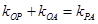 .
.
(1)求点P的轨迹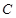 的方程;
的方程;
(2)设Q是轨迹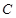 上异于点
上异于点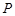 的一个点,若
的一个点,若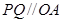 ,直线
,直线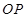 与
与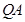 交于点M,探究是否存点P使得
交于点M,探究是否存点P使得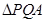 和
和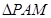 的面积满足
的面积满足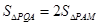 ,若存在,求出点P的坐标;若不存在,说明理由.
,若存在,求出点P的坐标;若不存在,说明理由.
 中,已知点
中,已知点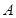
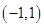 ,点P是动点,且三角形
,点P是动点,且三角形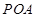 的三边所在直线
的三边所在直线的斜率满足
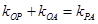 .
.
(1)求点P的轨迹
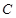 的方程;
的方程;(2)设Q是轨迹
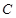 上异于点
上异于点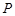 的一个点,若
的一个点,若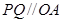 ,直线
,直线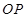 与
与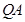 交于点M,探究是否存点P使得
交于点M,探究是否存点P使得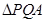 和
和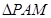 的面积满足
的面积满足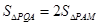 ,若存在,求出点P的坐标;若不存在,说明理由.
,若存在,求出点P的坐标;若不存在,说明理由.解:(1)设点 为所求轨迹上的任意一点,由
为所求轨迹上的任意一点,由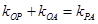 得,
得, ,
,

整理得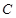 的方程为
的方程为 (
( 且
且 )。……4分(注:不写范围扣1分)
)。……4分(注:不写范围扣1分)
(2)解法一、设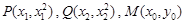 ,
,

 ,
,
 ,
,
 ,即
,即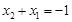 , ………6分
, ………6分

 三点共线,
三点共线,
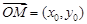 与
与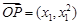 共线,∴
共线,∴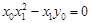 ,
,
由(1)知 ,故
,故 , ………8分
, ………8分
同理,由 与
与 共线,
共线,
∴ ,即
,即 ,
,
由(1)知 ,故
,故 ,…………9分
,…………9分
将 ,
, 代入上式得
代入上式得 ,
,
整理得 ,由
,由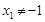 得
得 , …………11分
, …………11分
由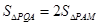 ,得到
,得到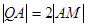 ,因为
,因为 ,所以
,所以 ,
,
由 ,得
,得 , ∴
, ∴ 的坐标为
的坐标为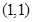 . …………14分
. …………14分
解法二、设 由
由 得
得 ,
,
故 ,即
,即 , ………6分
, ………6分
∴直线OP方程为: ①; …………8分
①; …………8分
直线QA的斜率为: ,
,
∴直线QA方程为: ,即
,即 , ② …10分
, ② …10分
联立①②,得 ,∴点M的横坐标为定值
,∴点M的横坐标为定值 。…………11分
。…………11分
由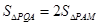 ,得到
,得到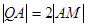 ,因为
,因为 ,所以
,所以 ,
,
由 ,得
,得 , ∴
, ∴ 的坐标为
的坐标为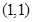 . …………14分
. …………14分
 为所求轨迹上的任意一点,由
为所求轨迹上的任意一点,由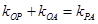 得,
得, ,
,
整理得
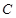 的方程为
的方程为 (
( 且
且 )。……4分(注:不写范围扣1分)
)。……4分(注:不写范围扣1分)(2)解法一、设
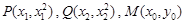 ,
,
 ,
,
 ,
,
 ,即
,即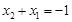 , ………6分
, ………6分
 三点共线,
三点共线,
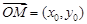 与
与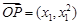 共线,∴
共线,∴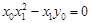 ,
,由(1)知
 ,故
,故 , ………8分
, ………8分同理,由
 与
与 共线,
共线,∴
 ,即
,即 ,
,由(1)知
 ,故
,故 ,…………9分
,…………9分将
 ,
, 代入上式得
代入上式得 ,
,整理得
 ,由
,由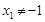 得
得 , …………11分
, …………11分由
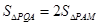 ,得到
,得到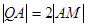 ,因为
,因为 ,所以
,所以 ,
,由
 ,得
,得 , ∴
, ∴ 的坐标为
的坐标为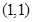 . …………14分
. …………14分解法二、设
 由
由 得
得 ,
,故
 ,即
,即 , ………6分
, ………6分∴直线OP方程为:
 ①; …………8分
①; …………8分直线QA的斜率为:
 ,
, ∴直线QA方程为:
 ,即
,即 , ② …10分
, ② …10分联立①②,得
 ,∴点M的横坐标为定值
,∴点M的横坐标为定值 。…………11分
。…………11分由
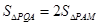 ,得到
,得到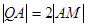 ,因为
,因为 ,所以
,所以 ,
,由
 ,得
,得 , ∴
, ∴ 的坐标为
的坐标为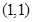 . …………14分
. …………14分考查向量知识在几何中的运用,实际上就是用坐标表示向量,再进行运算;(Ⅱ)的关键是确定出点M的横坐标为定值.
(Ⅰ)设点P(x,y)为所求轨迹上的任意一点,则由kOP+kOA=kPA得从而就可以得到轨迹C的方程;
(2)设出点PQ,M的坐标,然后利用三点共线得到坐标关系,进而再由面积得到点P的坐标。
(Ⅰ)设点P(x,y)为所求轨迹上的任意一点,则由kOP+kOA=kPA得从而就可以得到轨迹C的方程;
(2)设出点PQ,M的坐标,然后利用三点共线得到坐标关系,进而再由面积得到点P的坐标。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
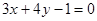 平行的直线方程是_______.
平行的直线方程是_______.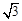 与l2: 2x+3y-6=0的交点M在第一象限,则l1的倾斜角的取值范围是( )
与l2: 2x+3y-6=0的交点M在第一象限,则l1的倾斜角的取值范围是( )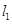 经过点A(3,a),B(a-1,2),直线
经过点A(3,a),B(a-1,2),直线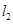 经过点C(1,2),D(-2,a+2),若
经过点C(1,2),D(-2,a+2),若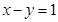 与
与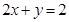 的交点,且平行于直
的交点,且平行于直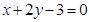 的直线方程。
的直线方程。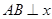 轴于点
轴于点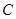 ,
,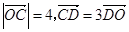 动点
动点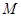 到直线
到直线 的距离是它到点
的距离是它到点 的距离的2倍.
的距离的2倍.
 为点
为点 轴正半轴的交点,直线
轴正半轴的交点,直线 交点
交点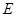 ,
,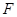 两点(
两点(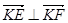 ,动点
,动点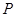 满足
满足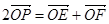 ,求直线
,求直线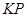 的斜率的取值范围.
的斜率的取值范围.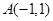 发出射向
发出射向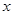 轴,被
轴,被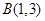 到反射线的距离为
到反射线的距离为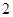 ,求反射线所在直线方程.
,求反射线所在直线方程.