已知命题p:?x∈R.2x＜3x,命题q:?x∈R.x3=-x2.则下列命题中为真命题的是( )A．￢p∧￢qB．p∧￢qC．￢p∧qD．p∧q 题目和参考答案——青夏教育精英家教网—

题目内容

10．已知命题p：?x∈R，2^x＜3^x；命题q：?x∈R，x³=-x²，则下列命题中为真命题的是（　　）

A．

￢p∧￢q

B．

p∧￢q

C．

￢p∧q

D．

p∧q

分析举反例说明命题p为假命题，则￢p为真命题．由x³=-x²，可得x=0或-1，从而得到命题q为真命题，由复合命题的真假得到答案．

解答解：因为x=-1时，2^-1＞3^-1，所以命题p：?x∈R，2^x＜3^x为假命题，则￢p为真命题．
因为x³=-x²，所以x=0或-1，所以命题q：?x∈R，x³=-x²为真命题．
则￢p∧q为真命题．
故选：C．

点评本题考查了复合命题的真假，考查了指数函数的性质及函数零点的判断方法，解答的关键是熟记复合命题的真值表，是基础题．

练习册系列答案

中考新航标初中重点知识总复习指导系列答案

1．已知向量$\overrightarrow a=（sinx，cosx），\overrightarrow b=（2{cos^2}\frac{φ}{2}-1，sinφ）$，且函数$f（x）=\overrightarrow a•\overrightarrow b（0＜φ＜π）$在x=π时取得最小值．
（Ⅰ）求φ的值；
（Ⅱ）在△ABC中，a，b，c分别是内角A，B，C的对边，若$a=3，\;f（A）=\frac{{\sqrt{6}}}{3}，B=A+\frac{π}{2}$，求b的值．

18．下列四个函数中，最小正周期为π，且关于直线x=-$\frac{5π}{12}$对称的函数是（　　）

A．

y=sin（$\frac{x}{2}+\frac{π}{3}$）

B．

y=sin（$\frac{x}{2}-\frac{π}{3}$）

C．

y=sin（2x-$\frac{π}{3}$）

D．

y=sin（2x+$\frac{π}{3}$）

5．

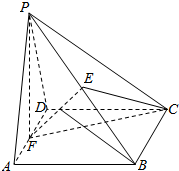如图，已知四棱锥P-ABCD的底面ABCD是边长为1的正方形，PD⊥底面ABCD，且PD=1，点E，F分别是棱PB，AD的中点．
（Ⅰ）求证：EF⊥平面PBC；
（Ⅱ）求多面体PDFEC的体积．

15．已知数列{a_n}满足${a_n}=sin\frac{nπ}{3}+{（{-1}）^n}（{n∈{N^*}}）$，则S₂₀₁₅=（　　）

2．已知$sin（π+α）=-\frac{4}{5}$，α∈（$\frac{π}{2}$，π）．
（1）求tan（π-α）的值；
（2）求$\frac{sin2α+1}{cos2α}$的值．

19．若x、y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤a}\\{y≥-1}\end{array}\right.$，其中a=${∫}_{0}^{π}$（sinx+cosx）dx，则z=x+2y的最大值为（　　）

20．已知命题p：函数y=log_0.5（x²+2x+a）的值域为R，命题q：函数y=-（5-2a）^x是R上的减函数．若p或q为真命题，p且q为假命题，则实数a的取值范围是什么？

试题分类