题目内容
设复数z1=1+2i，z2=1+i，记复数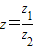
，则复数z的共轭复数
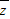在复平面内所对应的点位于（ ）A．第一象限
B．第二象限
C．第三象限
D．第四象限
【答案】分析：利用两个复数代数形式代数形式的乘除法求出z，再根据共轭复数的定义求出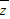
=
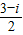，可得
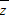在复平面内所对应的点的坐标，从而得出结论．
解答：解：由题意可得复数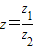
=
=
=
，
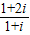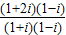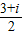故复数z的共轭复数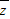
=
，
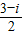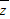在复平面内所对应的点的坐标为（
，-
），在第四象限，
故选D．
点评：本题主要考查两个复数代数形式的混合运算，复数与复平面内对应点之间的关系，属于基础题．
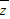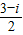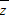=，可得在复平面内所对应的点的坐标，从而得出结论．解答：解：由题意可得复数
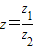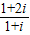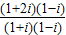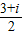===，故复数z的共轭复数
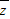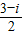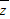=，在复平面内所对应的点的坐标为（，-），在第四象限，故选D．
点评：本题主要考查两个复数代数形式的混合运算，复数与复平面内对应点之间的关系，属于基础题．
练习册系列答案
相关题目
设复数z1=1-2i，z2=1+i，若复数z1=z•z2，则z=（ ）
| A、2+i | ||
| B、2-i | ||
C、-1-
| ||
D、
|
设复数z1=1-2i，z2=1+i，则复数z=
在复平面内对应的点位于（ ）
| z1 |
| z2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |