题目内容
(12分)已知函数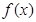 是定义在
是定义在 上的偶函数,已知当
上的偶函数,已知当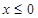 时,
时, .
.
(1)求函数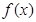 的解析式;
的解析式;
(2)求函数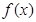 的单调递增区间;
的单调递增区间;
(3)求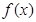 在区间
在区间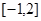 上的值域。
上的值域。
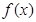 是定义在
是定义在 上的偶函数,已知当
上的偶函数,已知当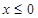 时,
时, .
.(1)求函数
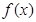 的解析式;
的解析式;(2)求函数
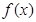 的单调递增区间;
的单调递增区间;(3)求
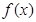 在区间
在区间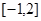 上的值域。
上的值域。(1)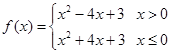
(2)函数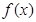 的单调递增区间为
的单调递增区间为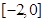 和
和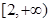
(3)值域为(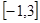
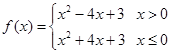
(2)函数
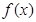 的单调递增区间为
的单调递增区间为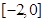 和
和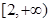
(3)值域为(
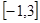
试题分析:解:(1)∵函数
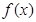 是定义在
是定义在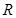 上的偶函数
上的偶函数∴对任意的
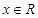 都有
都有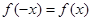 成立
成立∴当
 时,
时, 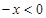 即
即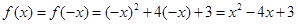
∴
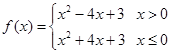 4分
4分(2)图形如图所示,函数
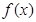 的单调递增区间为
的单调递增区间为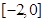 和
和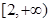 .(写成开区间也可以)8分
.(写成开区间也可以)8分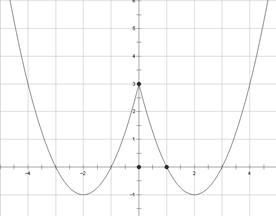
(3)值域为(
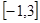 12分
12分点评:解决该试题的关键是利用二次函数的性质,以及奇偶性来分析得到函数的解析式,并求解单调性,属于基础题。

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
 (单位:元)关于当天需求量
(单位:元)关于当天需求量 (单位:份,
(单位:份, )的函数解析式.
)的函数解析式. 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求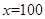 与函数
与函数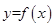 的图象的交点个数是 ( )
的图象的交点个数是 ( )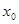 附近的左侧
附近的左侧 ,右侧
,右侧 ,那么
,那么 是极大值
是极大值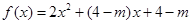 ,
,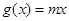 ,若对于任一实数
,若对于任一实数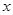 ,
,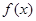 与
与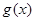 的值至少有一个为正数,则实数
的值至少有一个为正数,则实数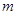 的取值范围是( )
的取值范围是( )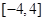
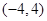
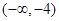
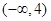
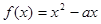 ,
,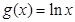
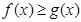 对于定义域内的
对于定义域内的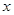 恒成立,求实数
恒成立,求实数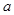 的取值范围;
的取值范围;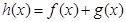 有两个极值点
有两个极值点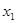 ,
,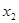 且
且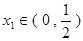 ,求证:
,求证: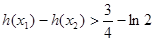 ;
;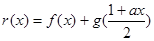 若对任意的
若对任意的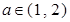 ,总存在
,总存在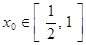 ,使不等式
,使不等式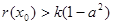 成立,求实数
成立,求实数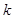 的取值范围.
的取值范围. 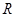 上的函数
上的函数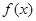 满足以下条件:
满足以下条件: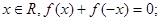 (2)对任意
(2)对任意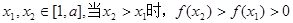 .
.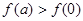 ;②
;②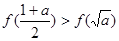 ;③
;③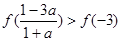 ;④
;④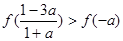 .其中一定成立的是 (请写出所有正确的序号)
.其中一定成立的是 (请写出所有正确的序号)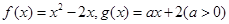 ,对
,对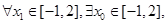 使
使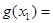
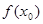 ,则
,则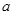 的取值范围是
的取值范围是
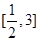
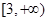
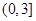
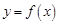 是函数
是函数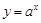
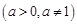 的反函数,且
的反函数,且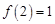 ,则
,则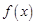 =
=