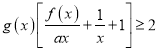题目内容
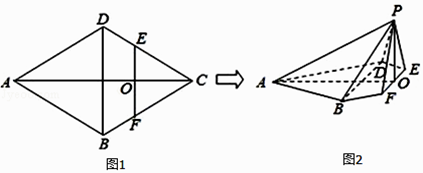
【题目】持续高温使漳州市多地出现气象干旱,城市用水紧张,为了宣传节约用水,某人准备在一片扇形区域(如图3)上按照图4的方式放置一块矩形ABCD区域宣传节约用水,其中顶点B,C在半径ON上,顶点A在半径OM上,顶点D在 ![]() 上,∠MON=
上,∠MON= ![]() ,ON=OM=10,m,设∠DON=θ,矩形ABCD的面积为S.
,ON=OM=10,m,设∠DON=θ,矩形ABCD的面积为S. 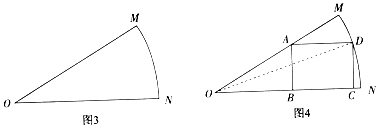
(Ⅰ)用含θ的式子表示DC,OB的长‘
(Ⅱ)若此人布置1m2的宣传区域需要花费40元,试将S表示为θ的函数,并求布置此矩形宣传栏最多要花费多少元钱?(精确到0.01)
(参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)
【答案】解:(Ⅰ)在△ODC中DC=10sinθ,在△OAB中,OB=10 ![]() sinθ;
sinθ;
(Ⅱ)在△ODC中OC=10cosθ,从而S=BC×CD=100(cosθsinθ﹣ ![]() sin2θ)(0<θ<
sin2θ)(0<θ< ![]() )
)
由S′=100(﹣sin2θ+cos2θ﹣2 ![]() sinθcosθ)=0得tan2θ=
sinθcosθ)=0得tan2θ= ![]() ,
,
由0<θ< ![]() ,得θ=
,得θ= ![]() ,易得θ=
,易得θ= ![]() 时,S的最大值为100(1﹣
时,S的最大值为100(1﹣ ![]() )≈13.4.
)≈13.4.
此人布置1m2的宣传区域需要花费40元,
∴布置此矩形宣传栏最多要花费13.4×40=536元钱.
【解析】(Ⅰ)直接在三角形中利用三角函数可以表示DC、OB的长;(Ⅱ)S=BC×CD,求出相应函数,再利用导数方法研究函数的最大值.

【题目】已知椭圆方程为 ![]() =1(a>0,b>0),其右焦点为F(4,0),过点F的直线交椭圆与A,B两点.若AB的中点坐标为(1,﹣1),则椭圆的方程为( )
=1(a>0,b>0),其右焦点为F(4,0),过点F的直线交椭圆与A,B两点.若AB的中点坐标为(1,﹣1),则椭圆的方程为( )
A.![]() =1
=1
B.![]() =1
=1
C.![]() +
+ ![]() =1
=1
D.![]() =1
=1
【题目】某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题:
分组 | 频数 | 频率 |
[60,70) | 10 | 0.1 |
[70,80) | 22 | 0.22 |
[80,90) | a | 0.38 |
[90,100] | 30 | c |
合计 | 100 | d |

(1)根据下面的频率分布表和频率分布直方图,求出a+d和b+c的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人?