题目内容
 P1,P2,…,Pn…顺次为函数y=
P1,P2,…,Pn…顺次为函数y=| 1 |
| x |
xn=2
| n |
xn=2
.| n |
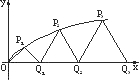
分析:利用△Qn-1PnQn为等腰直角三角形,且Pn为直角顶点,求出Pn点的横纵坐标,再根据Pn点为函数y=
(x>0)图象上的点,坐标满足函数y=
(x>0)的解析式,就可得到含xn-1,xn的等式,即数列{xn}的递推公式,再根据递推公式求出数列{xn}的通项公式即可.
| 1 |
| x |
| 1 |
| x |
解答:解:过Pn点作PnH⊥x轴,垂足为H,
∵△Qn-1PnQn为等腰直角三角形,且Pn为直角顶点,
∴|PnH|=
|Qn-1Qn|=
,
∴Pn点的纵坐标为
∵△Qn-1PnQn为等腰直角三角形,且Pn为直角顶点,
∴H点为线段Qn-1Qn的中点,
∴H点横坐标为
∵PnH⊥x轴,∴Pn点的横坐标也为
,
∵Pn点为函数y=
(x>0)图象上的点,
∴Pn(
,
)
∴
=
∴xn2-xn-12=4∴xn2=x12+4(n-1)=4n
∴xn=2
故答案为xn=2
∵△Qn-1PnQn为等腰直角三角形,且Pn为直角顶点,
∴|PnH|=
| 1 |
| 2 |
| xn-xn-1 |
| 2 |
∴Pn点的纵坐标为
| xn-xn-1 |
| 2 |
∵△Qn-1PnQn为等腰直角三角形,且Pn为直角顶点,
∴H点为线段Qn-1Qn的中点,
∴H点横坐标为
| xn+xn-1 |
| 2 |
∵PnH⊥x轴,∴Pn点的横坐标也为
| xn+xn-1 |
| 2 |
∵Pn点为函数y=
| 1 |
| x |
∴Pn(
| xn+xn-1 |
| 2 |
| 2 |
| xn+xn-1 |
∴
| 2 |
| xn+xn-1 |
| xn-xn-1 |
| 2 |
∴xn2-xn-12=4∴xn2=x12+4(n-1)=4n
∴xn=2
| n |
故答案为xn=2
| n |
点评:本题是函数与数列的综合,根据点在函数图象上,以及点之间的关系,找到坐标之间的关系,即数列的递推公式,再由递推公式求通项公式,属于综合题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
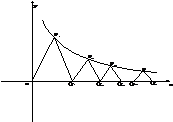
 如图,设P0是抛物线y=x2上一点,且在第一象限.过点P0作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P0确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论:
如图,设P0是抛物线y=x2上一点,且在第一象限.过点P0作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P0确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论: