题目内容
已知m∈R,对p:x1和x2是方程x2-ax-2=0的两个根,不等式|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立;q:函数f(x)=3x2+2mx+m+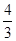 有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围.
【答案】
【解析】
试题分析:解:由题设知x1+x2=a,x1x2=-2,
∴|x1-x2|==.
a∈[1,2]时,的最小值为3,要使|m-5|≤|x1-x2|对任意实数a∈[1,2]恒成立,只需|m-5|≤3,即2≤m≤8.
由已知,得f(x)=3x2+2mx+m+=0的判别式Δ=4m2-12(m+)=4m2-12m-16>0,得m<-1或m>4,
综上,要使“p且q”为假命题、“p或q”为真命题,只需p真q假或p假q真,即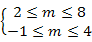 或
或 解得实数m的取值范围是
解得实数m的取值范围是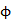 .
.
考点:逻辑联结词
点评:逻辑联结词有三个:且、或和非。在且命题中,只有两个命题都为真时,且命题才为真,而在或命题中,只要一个命题为真时,或命题就为真。

练习册系列答案
相关题目
 有两个不同的零点.求使“p且q”为真命题的实数m的取值范围.
有两个不同的零点.求使“p且q”为真命题的实数m的取值范围. 有两个不同的零点.求使“p且q”为真命题的实数m的取值范围.
有两个不同的零点.求使“p且q”为真命题的实数m的取值范围.