题目内容
已知m∈R，对p：x1和x2是方程x2-ax-2=0的两个根，不等式|m-5|≤|x1-x2|对任意实数a∈[1，2]恒成立；q：函数f（x）=3x2+2mx+m+
有两个不同的零点．求使“p且q”为真命题的实数m的取值范围．
| 4 |
| 3 |
由题设x1+x2=a，x1x2=-2，
∴|x1-x2|=
=
．
当a∈[1，2]时，
的最小值为3．
要使|m-5|≤|x1-x2|对任意实数a∈[1，2]恒成立，只须|m-5|≤3，即2≤m≤8．
由已知，得f（x）=3x2+2mx+m+
=0的判别式
△=4m2-12（m+
）=4m2-12m-16＞0，
得m＜-1或m＞4．
综上，要使“p且q”为真命题，只需P真Q真，即
，
解得实数m的取值范围是（4，8]．
∴|x1-x2|=
| (x1+x2)2-4x1x2 |
| a2+8 |
当a∈[1，2]时，
| a2+8 |
要使|m-5|≤|x1-x2|对任意实数a∈[1，2]恒成立，只须|m-5|≤3，即2≤m≤8．
由已知，得f（x）=3x2+2mx+m+
| 4 |
| 3 |
△=4m2-12（m+
| 4 |
| 3 |
得m＜-1或m＞4．
综上，要使“p且q”为真命题，只需P真Q真，即
|
解得实数m的取值范围是（4，8]．
练习册系列答案
快捷英语周周练系列答案
相关题目
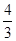有两个不同的零点.求使“p且q”为假命题、“p或q”为真命题的实数m的取值范围．
有两个不同的零点．求使“p且q”为真命题的实数m的取值范围．
有两个不同的零点．求使“p且q”为真命题的实数m的取值范围．