题目内容
已知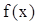 为奇函数,若
为奇函数,若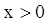 时,
时,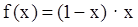 ,则
,则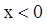 时,
时,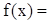 ( )
( )
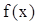 为奇函数,若
为奇函数,若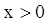 时,
时,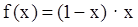 ,则
,则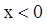 时,
时,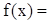 ( )
( )A.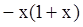 | B.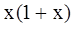 | C.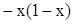 | D.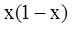 |
B
因为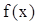 为奇函数,若
为奇函数,若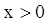 时,
时,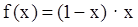 ,则
,则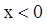 时,
时,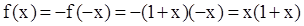 ,故选B
,故选B
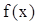 为奇函数,若
为奇函数,若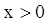 时,
时,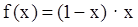 ,则
,则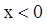 时,
时,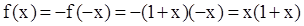 ,故选B
,故选B
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
题目内容
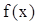 为奇函数,若
为奇函数,若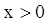 时,
时,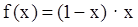 ,则
,则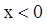 时,
时,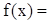 ( )
( )A.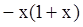 | B.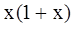 | C.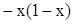 | D.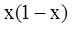 |
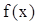 为奇函数,若
为奇函数,若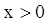 时,
时,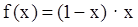 ,则
,则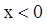 时,
时,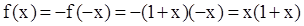 ,故选B
,故选B
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案