题目内容
△ABC中，AB=3，BC=5，CA=7，点D是边AC上的点，且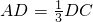
，则
=________．
-
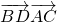分析：利用两个向量的数量积的定义求出=（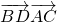
）•
=-21cosA+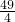
．
余弦定理求出cosA代入可求得结果．
解答：由题意得 AD=
AC=
，=（ ）•=
+
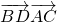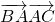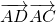
=BA•AC•（-cosA）+×7=-21cosA+．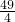
△ABC中，由余弦定理得 25=9+49-2×3×7cosA，∴cosA=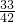
，
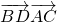∴=-21×+=-，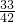
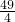故答案为：-．
点评：本题考查两个向量的数量积的定义，余弦定理的应用，计算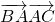是本题得易错点．
分析：利用两个向量的数量积的定义求出
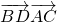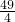=（ ）•=-21cosA+．余弦定理求出cosA代入可求得结果．
解答：由题意得 AD=
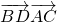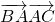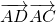
AC=，=（ ）•=+ =BA•AC•（-cosA）+
×7=-21cosA+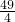．△ABC中，由余弦定理得 25=9+49-2×3×7cosA，∴cosA=
，∴
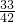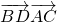=-21×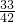+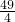=-，故答案为：-
．点评：本题考查两个向量的数量积的定义，余弦定理的应用，计算
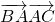是本题得易错点． 
练习册系列答案
相关题目