题目内容

在△ABC中，AB=
3
，BC=2，A=
π
2
，如果不等式|
BA
-t
BC
|≥|
AC
|恒成立，试求实数t的取值范围．
分析：利用解直角三角形求出AC边，据向量的平方等于模的平方，将已知等式平方得到关于t的不等式，解不等式求出t的范围．
解答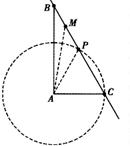：解：由题意得
|AC|
=
|BC|
2-
|AC|
2
=1，cos∠ABC=
3
2

∵|
BA
-t
BC
|≥|
AC
|，可得|
BA
-t
BC
|2≥|
AC
|2
∴
|BA|
2-2t
BA
•
BC 
+t2
|BC|
2≥|
AC
|2，
即3-2t•
3
•2•
3
2
+t2•22≥12，
解之得t≤
1
2
或t≥1．
即实数t的取值范围为（-∞，
1
2
]∪[1，+∞）
点评：本题给出直角三角形ABC，在已知向量等式的情况下求参数的取值范围．着重考查解直角三角形和向量的数量积与向量模的性质等知识，属于中档题．
练习册系列答案
相关题目
在△ABC中，AB=AC，D、E分别是AB、AC的中点，则（　　）
在△ABC中，AB=4，AC=2，S△ABC=2
3
．
（1）求△ABC外接圆的面积．
（ 2）求cos（2B+
π
3
）的值．
在△ABC中，AB=a，AC=b，当
a
•
b
＜0时，△ABC为
钝角三角形
钝角三角形
．
在△ABC中，AB=2，BC=3，AC=
7
，则△ABC的面积为
3
3
2
3
3
2
，△ABC的外接圆的面积为
7π
3
7π
3
．
在△ABC中，
AB
=
a
，
AC
=
b
，M为AB的中点，
BN
=
1
3
BC
，则
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网