题目内容
某企业有A、B两种型号的家电产品参加家电下乡活动,若企业投放A、B两种型号家电产品的价值分别为a、b万元,则农民购买家电产品获得的补贴分别为tlna万元、
b万元(t>0且为常数).已知该企业投放总价值为100万元的A、B两种型号的家电产品,且A、B两种型号的投放金额都不低于10万元.
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)问A、B两种型号的家电产品各投放多少万元时,农民得到的总补贴最多?
| 1 | 10 |
(1)请你选择自变量,将这次活动中农民得到的总补贴表示为它的函数,并求其定义域;
(2)问A、B两种型号的家电产品各投放多少万元时,农民得到的总补贴最多?
分析:(1)先投放A型产品的金额的x万元,则投放B型产品的金额为(100-x)万元,根据农民购买家电产品获得的补贴分别为tlna万元、
b万元(t>0且为常数),即可得到农民得到的总补贴的函数解析式;
(2)对于(1)中求得的函数,取导函数,分类讨论确定单调性,从而可求其最大值.
| 1 |
| 10 |
(2)对于(1)中求得的函数,取导函数,分类讨论确定单调性,从而可求其最大值.
解答:解:(1)设投放A型产品的金额的x万元,则投放B型产品的金额为(100-x)万元,
农民得到的总补贴f(x)=tlnx+
(100-x)=tlnx-
x+10
∵x≥10,100-x≥10,∴10≤x≤90,∴其定义域为[10,90];
(2)f′(x)=
-
=
(10≤x≤90,t>0),令f′(x)=0,得x=10t
1°若10t≤10,即0<t≤1,则f′(x)≤0,∴f(x)在[10,90]为减函数,当x=10时,f(x)有最大值;
2°若10<10t<90,即1<t<9,则f(x)在[10,10t]是增函数,在[10t,90]是减函数,当x=10t时,f(x)有最大值;
3°若10t≥90即t≥9,f′(x)≥0,则f(x)在[10,90]是增函数,∴当x=90时,f(x)有最大值.
因此,当0<t≤1时,投放A型产品10万元,投放B型产品90万元;当1<t<9时,投放A型产品10t万元,投放B型产品(100-10t)万元;当t≥9时,投放A型产品90万元,投放B型产品10万元,农民得到的总补贴最大.
农民得到的总补贴f(x)=tlnx+
| 1 |
| 10 |
| 1 |
| 10 |
∵x≥10,100-x≥10,∴10≤x≤90,∴其定义域为[10,90];
(2)f′(x)=
| t |
| x |
| 1 |
| 10 |
| 10t-x |
| 10x |
1°若10t≤10,即0<t≤1,则f′(x)≤0,∴f(x)在[10,90]为减函数,当x=10时,f(x)有最大值;
2°若10<10t<90,即1<t<9,则f(x)在[10,10t]是增函数,在[10t,90]是减函数,当x=10t时,f(x)有最大值;
3°若10t≥90即t≥9,f′(x)≥0,则f(x)在[10,90]是增函数,∴当x=90时,f(x)有最大值.
因此,当0<t≤1时,投放A型产品10万元,投放B型产品90万元;当1<t<9时,投放A型产品10t万元,投放B型产品(100-10t)万元;当t≥9时,投放A型产品90万元,投放B型产品10万元,农民得到的总补贴最大.
点评:本题主要考查函数模型的选择与应用、利用导数研究函数的单调性及函数的最值,考查运算求解能力,分类讨论思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
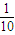 a,mln(b+1)万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
a,mln(b+1)万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.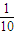 a,mln(b+1)万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
a,mln(b+1)万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元. 万元(m >
0且为常数).已知该企业投放总价值为10万元的A、B
万元(m >
0且为常数).已知该企业投放总价值为10万元的A、B 万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.
万元(m>0且为常数).已知该企业投放总价值为10万元的A、B两种型号的电视机,且A、B两种型号的投放金额都不低于1万元.