题目内容
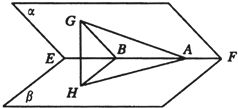 平面角为锐角的二面角α-EF-β,A∈EF,AG?α,∠GAE=45°,若AG与β所成角为30°,求二面角α-EF-β的平面角.
平面角为锐角的二面角α-EF-β,A∈EF,AG?α,∠GAE=45°,若AG与β所成角为30°,求二面角α-EF-β的平面角.分析:如图所示.过GH⊥β,垂足为H点,作HB⊥EF交EF于点B,连接AH、GB.则EF⊥BG,∠HBG是二面角α-EF-β的平面角.在Rt△AGH中,取GH=1,可得GA,在Rt△ABG中,可得BG.在Rt△GBH中,sin∠GBH=
即可得出.
| GH |
| GB |
解答:解:如图所示.
作GH⊥β,垂足为H点,作HB⊥EF交EF于点B,连接AH、GB.
则EF⊥BG,∠GAH=30°,∠HBG是二面角α-EF-β的平面角.
在Rt△AGH中,取GH=1,则AG=2.
在Rt△ABG中,∵∠BGA=45°,∴BG=
.
在Rt△GBH中,sin∠GBH=
=
=
,
∵∠GBH为锐角,∴∠GBH=45°.

作GH⊥β,垂足为H点,作HB⊥EF交EF于点B,连接AH、GB.
则EF⊥BG,∠GAH=30°,∠HBG是二面角α-EF-β的平面角.
在Rt△AGH中,取GH=1,则AG=2.
在Rt△ABG中,∵∠BGA=45°,∴BG=
| 2 |
在Rt△GBH中,sin∠GBH=
| GH |
| GB |
| 1 | ||
|
| ||
| 2 |
∵∠GBH为锐角,∴∠GBH=45°.
点评:本题考查了二面角、线面角的作法和求法、线面垂直的判定与性质、三垂线定理及其逆定理等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
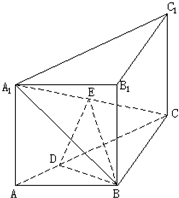 (2005•朝阳区一模)直三棱柱ABC-A1B1C1中,AB⊥BC,E是A1C的中点,ED⊥A1C且交AC于D,
(2005•朝阳区一模)直三棱柱ABC-A1B1C1中,AB⊥BC,E是A1C的中点,ED⊥A1C且交AC于D, α,∠GAE=
α,∠GAE=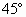 ,若AG与β所成角为
,若AG与β所成角为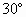 ,则二面角α-EF-β的平面角为________.
,则二面角α-EF-β的平面角为________.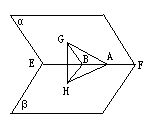
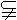 a,
a,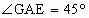 .若AG与β所成的角为30°.求二面角
.若AG与β所成的角为30°.求二面角 的平面角.
的平面角.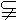 a,
a,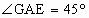 .若AG与β所成的角为30°.求二面角
.若AG与β所成的角为30°.求二面角 的平面角.
的平面角.