题目内容
设函数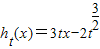 ,若有且仅有一个正实数x,使得h7(x)≥ht(x)对任意的正数t都成立,则x=( )
,若有且仅有一个正实数x,使得h7(x)≥ht(x)对任意的正数t都成立,则x=( )A.5
B.
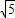
C.3
D.
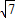
【答案】分析:构造函数g(t)=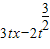 ,则g′(t)=
,则g′(t)=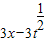 ,分析可得g(
,分析可得g(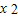 )即为函数g(t)=
)即为函数g(t)=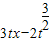 的最大值,则可将已知化为
的最大值,则可将已知化为 =7.
=7.
解答:解:令g(t)=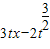 -(
-(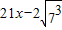 ),则g′(t)=
),则g′(t)=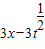
令g′(t)=0,则t=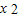 ,由此得t<
,由此得t<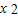 ,g′(t)>0,t>
,g′(t)>0,t>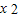 ,g′(t)<0,
,g′(t)<0,
可得g(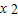 )即为函数g(t)=
)即为函数g(t)=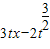 的最大值,
的最大值,
若有且仅有一个正实数x,使得h7(x)≥ht(x)对任意的正数t都成立,
则g(7)为函数g(t)的最大值,且7是函数g(t)的唯一最大值
∴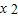 =7
=7
又∵x为正实数,
故x=
故选D
点评:本题考查的知识点是函数恒成立问题,其中构造以t为自变量的新函数,并分析函数的单调性,进而将已知转化为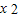 =7是解答的关键.
=7是解答的关键.
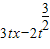 ,则g′(t)=
,则g′(t)=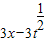 ,分析可得g(
,分析可得g(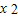 )即为函数g(t)=
)即为函数g(t)=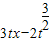 的最大值,则可将已知化为
的最大值,则可将已知化为 =7.
=7.解答:解:令g(t)=
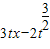 -(
-(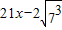 ),则g′(t)=
),则g′(t)=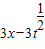
令g′(t)=0,则t=
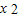 ,由此得t<
,由此得t<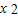 ,g′(t)>0,t>
,g′(t)>0,t>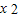 ,g′(t)<0,
,g′(t)<0,可得g(
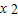 )即为函数g(t)=
)即为函数g(t)=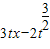 的最大值,
的最大值,若有且仅有一个正实数x,使得h7(x)≥ht(x)对任意的正数t都成立,
则g(7)为函数g(t)的最大值,且7是函数g(t)的唯一最大值
∴
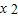 =7
=7又∵x为正实数,
故x=

故选D
点评:本题考查的知识点是函数恒成立问题,其中构造以t为自变量的新函数,并分析函数的单调性,进而将已知转化为
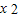 =7是解答的关键.
=7是解答的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目