题目内容
设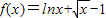 ,证明:
,证明:(Ⅰ)当x>1时,f(x)<
 ( x-1);
( x-1);(Ⅱ)当1<x<3时,
 .
.
【答案】分析:(Ⅰ)证法一,记g(x)=lnx+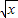 -1-
-1- (x-1),可得到g′(x)=
(x-1),可得到g′(x)=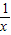 +
+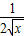 -
- <0,从而g(x)为减函数,又g(1)=0,当x>1时,g(x)<g(1),问题解决;
<0,从而g(x)为减函数,又g(1)=0,当x>1时,g(x)<g(1),问题解决;
证法二,利用均值不等式,可证得,当x>1时,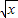 <
<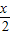 +
+ .①,令k(x)=lnx-x+1,同理可证k(x)为减函数,于是有lnx<x-1②,由①②可证得结论;
.①,令k(x)=lnx-x+1,同理可证k(x)为减函数,于是有lnx<x-1②,由①②可证得结论;
(Ⅱ)记h(x)=f(x)-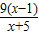 ,可求得h′(x)=
,可求得h′(x)=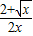 -
-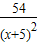 <
<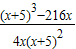 <0(1<x<3),从而h(x)在(1,3)内是递减函数,又由h(1)=0,得h(x)<0,从而证得结论;
<0(1<x<3),从而h(x)在(1,3)内是递减函数,又由h(1)=0,得h(x)<0,从而证得结论;
解答:证明:(Ⅰ)(证法一):
记g(x)=lnx+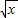 -1-
-1- (x-1),则当x>1时,g′(x)=
(x-1),则当x>1时,g′(x)=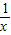 +
+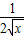 -
- <0,
<0,
又g(1)=0,有g(x)<0,即f(x)< ( x-1);…4′
( x-1);…4′
(证法二)由均值不等式,当x>1时,2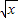 <x+1,故
<x+1,故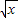 <
<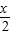 +
+ .①
.①
令k(x)=lnx-x+1,则k(1)=0,k′(x)=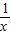 -1<0,故k(x)<0,即lnx<x-1②
-1<0,故k(x)<0,即lnx<x-1②
由①②得当x>1时,f(x)< ( x-1);
( x-1);
(Ⅱ)记h(x)=f(x)-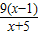 ,由(Ⅰ)得,
,由(Ⅰ)得,
h′(x)=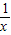 +
+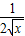 -
-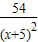
=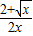 -
-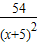
<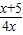 -
-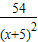
=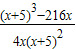 ,
,
令g(x)=(x+5)3-216x,则当1<x<3时,g′(x)=3(x+5)2-216<0,
∴g(x)在(1,3)内是递减函数,又由g(1)=0,得g(x)<0,
∴h′(x)<0,…10′
因此,h(x)在(1,3)内是递减函数,又由h(1)=0,得h(x)<0,
于是,当1<x<3时,f(x)<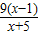 …12′
…12′
点评:本题考查利用导数求闭区间上函数的最值,着重考查构造函数的思想,考查分析、转化与综合计算与应用解决问题的能力,属于难题.
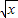 -1-
-1- (x-1),可得到g′(x)=
(x-1),可得到g′(x)=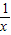 +
+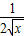 -
- <0,从而g(x)为减函数,又g(1)=0,当x>1时,g(x)<g(1),问题解决;
<0,从而g(x)为减函数,又g(1)=0,当x>1时,g(x)<g(1),问题解决;证法二,利用均值不等式,可证得,当x>1时,
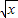 <
<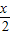 +
+ .①,令k(x)=lnx-x+1,同理可证k(x)为减函数,于是有lnx<x-1②,由①②可证得结论;
.①,令k(x)=lnx-x+1,同理可证k(x)为减函数,于是有lnx<x-1②,由①②可证得结论;(Ⅱ)记h(x)=f(x)-
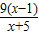 ,可求得h′(x)=
,可求得h′(x)=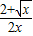 -
-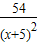 <
<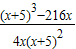 <0(1<x<3),从而h(x)在(1,3)内是递减函数,又由h(1)=0,得h(x)<0,从而证得结论;
<0(1<x<3),从而h(x)在(1,3)内是递减函数,又由h(1)=0,得h(x)<0,从而证得结论;解答:证明:(Ⅰ)(证法一):
记g(x)=lnx+
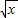 -1-
-1- (x-1),则当x>1时,g′(x)=
(x-1),则当x>1时,g′(x)=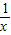 +
+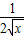 -
- <0,
<0,又g(1)=0,有g(x)<0,即f(x)<
 ( x-1);…4′
( x-1);…4′(证法二)由均值不等式,当x>1时,2
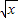 <x+1,故
<x+1,故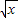 <
<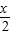 +
+ .①
.①令k(x)=lnx-x+1,则k(1)=0,k′(x)=
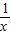 -1<0,故k(x)<0,即lnx<x-1②
-1<0,故k(x)<0,即lnx<x-1②由①②得当x>1时,f(x)<
 ( x-1);
( x-1);(Ⅱ)记h(x)=f(x)-
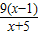 ,由(Ⅰ)得,
,由(Ⅰ)得,h′(x)=
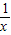 +
+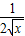 -
-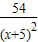
=
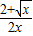 -
-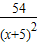
<
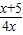 -
-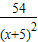
=
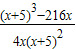 ,
,令g(x)=(x+5)3-216x,则当1<x<3时,g′(x)=3(x+5)2-216<0,
∴g(x)在(1,3)内是递减函数,又由g(1)=0,得g(x)<0,
∴h′(x)<0,…10′
因此,h(x)在(1,3)内是递减函数,又由h(1)=0,得h(x)<0,
于是,当1<x<3时,f(x)<
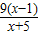 …12′
…12′点评:本题考查利用导数求闭区间上函数的最值,着重考查构造函数的思想,考查分析、转化与综合计算与应用解决问题的能力,属于难题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 (2012•上高县模拟)如图,等腰△ABC的底边AB=6,高CD=3,点E是线段BD上异于点B、D的动点,点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACFE的体积.
(2012•上高县模拟)如图,等腰△ABC的底边AB=6,高CD=3,点E是线段BD上异于点B、D的动点,点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE,记BE=x,V(x)表示四棱锥P-ACFE的体积. 的定义域为R,当x<0时,
的定义域为R,当x<0时,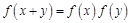 .
.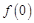 ,判断并证明函数
,判断并证明函数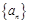 满足
满足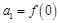 ,且
,且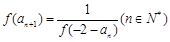 ,
,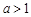 时,不等式
时,不等式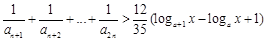 对不小于2的正整数
对不小于2的正整数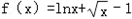 ,证明:
,证明: ( x-1);
( x-1);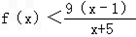 。
。