题目内容
已知曲线的参数方程为
|
分析:先表示出曲线上的点到原点的距离,进而利用辅角公式化简整理,进而根据正弦函数的性质求得距离的最小值.
解答:解:曲线上的点到原点的距离为
=
≥
=5-
故答案为;5-
| (5cosθ+1) 2+(5sinθ-1) 2 |
25-10
|
25-10
|
| 2 |
故答案为;5-
| 2 |
点评:本题主要考查了曲线的参数方程,两点间的距离公式,辅角公式的化简求值.考查了学生数形结合的思想和转化和化归的思想.

练习册系列答案
相关题目
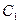 的参数方程为
的参数方程为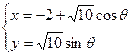 (
( 为参数),曲线
为参数),曲线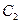 的极坐标方程为
的极坐标方程为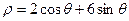 .
. 的参数方程为
的参数方程为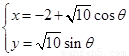 (
(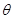 为参数),曲线
为参数),曲线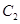 的极坐标方程
的极坐标方程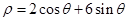 .
.