题目内容
已知曲线 的参数方程为
的参数方程为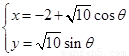 (
(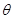 为参数),曲线
为参数),曲线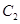 的极坐标方程
的极坐标方程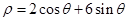 .
.
(Ⅰ)将曲线 的参数方程化为普通方程,将曲线
的参数方程化为普通方程,将曲线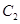 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)曲线 ,
,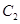 是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
是否相交,若相交请求出公共弦的长,若不相交,请说明理由.
【答案】
(Ⅰ)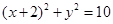 和
和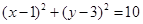 ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)参数方程化为普通方程,消去参数即可,极坐标方程化为直角坐标方程,利用两者坐标之间的关系互化,此类问题一般较为容易;(Ⅱ)由(Ⅰ)知,两曲线都是圆,判断两圆的位置关系,利用圆心距与两半径大小关系判断即可,两圆相交,公共弦和易求.
试题解析:(Ⅰ)由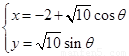 消去参数
消去参数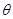 ,得
,得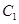 的普通方程为:
的普通方程为: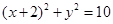 ;
;
由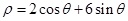 ,得
,得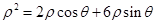 ,化为直角坐标方程为
,化为直角坐标方程为 即
即
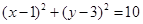 .
5分
.
5分
(Ⅱ)∵圆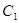 的圆心为
的圆心为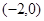 ,圆
,圆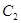 的圆心为
的圆心为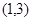
∴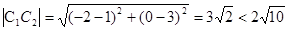 ,∴两圆相交
,∴两圆相交
设相交弦长为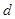 ,因为两圆半径相等,所以公共弦平分线段
,因为两圆半径相等,所以公共弦平分线段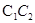
∴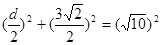
∴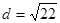 ∴公共弦长为
∴公共弦长为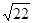 10分
10分
考点:极坐标方程和参数方程.

练习册系列答案
相关题目
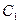 的参数方程为
的参数方程为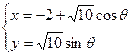 (
( 为参数),曲线
为参数),曲线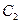 的极坐标方程为
的极坐标方程为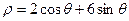 .
.