题目内容
求“方程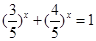 的解”有如下解题思路:设
的解”有如下解题思路:设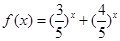 ,则
,则 在
在 上单调递减,且
上单调递减,且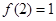 ,所以原方程有唯一解
,所以原方程有唯一解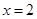 .类比上述解题思路,方程
.类比上述解题思路,方程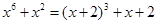 的解为 .
的解为 .
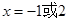
解析试题分析:类比上述解题思路,设f(x)=x3+x,由于f′(x)=3x2+1≥0,则f(x)在R上单调递增,
由x6+x2=(x+2)3+(x+2)即(x2)3+x2=(x+2)3+(x+2),∴x2=x+2,解之得,x=-1或x=2.
所以方程x6+x2=(x+2)3+(x+2)的解集为{-1,2}.故答案为:{-1,2}.
考点:类比

练习册系列答案
相关题目
 ,…,根据上述规律,第五个等式为______________.
,…,根据上述规律,第五个等式为______________.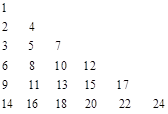
 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数,如
个数,如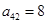 .若
.若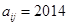 ,则
,则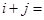 .
.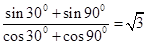 ,
,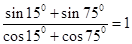 ,
,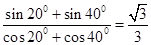 .照此规律,对于一般的角
.照此规律,对于一般的角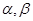 ,有等式 .
,有等式 .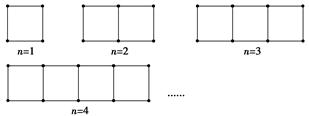
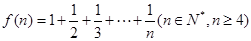 ,经计算得
,经计算得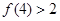 ,
,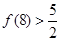 ,
, ,
,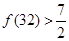
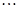 ,观察上述结果,可归纳出的一般结论为 .
,观察上述结果,可归纳出的一般结论为 .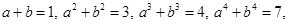
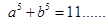 则
则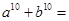 ___________.
___________.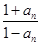 (n∈N*),则a3=________,a1·a2·a3·…·a2014=________.
(n∈N*),则a3=________,a1·a2·a3·…·a2014=________.