题目内容
下列说法:①命题“
 ”的否定是“?x∈R,2x>0”;
”的否定是“?x∈R,2x>0”;②关于x的不等式
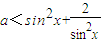 恒成立,则a的取值范围是a<3;
恒成立,则a的取值范围是a<3;③函数f(x)=alog2|x|+x+b为奇函数的充要条件是a+b=0;
④(1+kx2)10(k为正整数)的展开式中,x16的系数小于90,则k的值为2.
其中正确的个数是( )
A.1
B.2
C.3
D.4
【答案】分析:据含量词的命题的否定判断出①对
不等式恒成立转化成函数的最值判断出②对
通过举反例判断出③错
利用二项展开式的通项求出展开式中x16的系数列出不等式求出k的范围,判断出④错
解答:解:对于①,据含逻辑连接词的命题否定形式:“存在”变为“任意”,结论否定,故①对
对于②∵ ,∴
,∴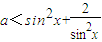 恒成立时,a<3故②对
恒成立时,a<3故②对
对于③当a=1,b=-1时,虽然有a+b=0,但f(x)不是奇函数故③错
对于④(1+kx2)10(k为正整数)的展开式中,x16的系数为k8C108<90解得k8<2故④错
故选B
点评:本题考查含量词的命题的否定、不等式恒成立问题、二项展开式的通项公式.
不等式恒成立转化成函数的最值判断出②对
通过举反例判断出③错
利用二项展开式的通项求出展开式中x16的系数列出不等式求出k的范围,判断出④错
解答:解:对于①,据含逻辑连接词的命题否定形式:“存在”变为“任意”,结论否定,故①对
对于②∵
 ,∴
,∴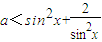 恒成立时,a<3故②对
恒成立时,a<3故②对对于③当a=1,b=-1时,虽然有a+b=0,但f(x)不是奇函数故③错
对于④(1+kx2)10(k为正整数)的展开式中,x16的系数为k8C108<90解得k8<2故④错
故选B
点评:本题考查含量词的命题的否定、不等式恒成立问题、二项展开式的通项公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目