题目内容
下列说法:
①命题“存在x0∈R,使2x0≤0”的否定是
“对任意的x ∈R,2x >0”;
②若回归直线方程为
=1.5x+45,x∈{1,5,7,13,19},则
=58.5;
③设函数f(x)=x+ln(x+
),则对于任意实数a和b,a+b<0是f(a)+f(b))<0的充要条件;
④“若x∈R,则|x|<1⇒-1<x<1”类比推出“若z∈C,则|z|<1⇒-1<z<1”
其中正确的个数是( )
①命题“存在x0∈R,使2x0≤0”的否定是
“对任意的x ∈R,2x >0”;
②若回归直线方程为
| ? |
| y |
. |
| y |
③设函数f(x)=x+ln(x+
| 1+x2 |
④“若x∈R,则|x|<1⇒-1<x<1”类比推出“若z∈C,则|z|<1⇒-1<z<1”
其中正确的个数是( )
分析:对于①利用命题的否定方法,特称命题转化为全称性命题;
对于②,由于
=9,∴
=58.5;
对于③易知函数为单调增函数;
对于④,由实数推广到复数,结论不成立,故错误.
对于②,由于
. |
| x |
. |
| y |
对于③易知函数为单调增函数;
对于④,由实数推广到复数,结论不成立,故错误.
解答:解:对于①利用命题的否定方法,特称命题转化为全称性命题,故正确;
对于②,由于
=9,∴
=58.5,故正确;
对于③易知函数为单调增函数,故任意实数a和b,a+b<0是f(a)+f(b))<0充要条件,故正确;
对于④,由实数推广到复数,结论不成立,故错误.
故选C.
对于②,由于
. |
| x |
. |
| y |
对于③易知函数为单调增函数,故任意实数a和b,a+b<0是f(a)+f(b))<0充要条件,故正确;
对于④,由实数推广到复数,结论不成立,故错误.
故选C.
点评:本题主要考查命题真假的判断,对于每个命题一一判断是关键,综合性强,有一定的难度

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
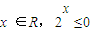 ”的否定是“对任意的
”的否定是“对任意的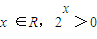 ”;
”;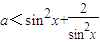 恒成立,则a的取值范围是a<3;
恒成立,则a的取值范围是a<3;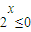 ”的否定是
”的否定是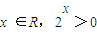 ”;
”;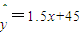 ,x∈{1,5,7,13,19},则
,x∈{1,5,7,13,19},则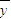 =58.5;
=58.5;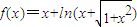 ,则对于任意实数a和b,a+b<0是f(a)+f(b))<0的充要条件;
,则对于任意实数a和b,a+b<0是f(a)+f(b))<0的充要条件;