题目内容
下列说法:
①命题“存在x ∈R,2x ≤0”的否定是“对任意的x ∈R,2x >0”;
②关于x的不等式a<sin2x+
恒成立,则a的取值范围是a<3;
③函数f(x)=alog2|x|+x+b为奇函数的充要条件是a+b=0;
其中正确的个数是( )
①命题“存在x ∈R,2x ≤0”的否定是“对任意的x ∈R,2x >0”;
②关于x的不等式a<sin2x+
| 2 |
| sin2x |
③函数f(x)=alog2|x|+x+b为奇函数的充要条件是a+b=0;
其中正确的个数是( )
分析:①根据含量词的命题的否定对①进行判断;
②不等式恒成立转化成函数的最值进行判断出;
③通过举反例对③进行判断;
②不等式恒成立转化成函数的最值进行判断出;
③通过举反例对③进行判断;
解答:解:对于①,据含逻辑连接词的命题否定形式:“存在”变为“任意”,结论否定,故①对
对于②∵0≤sin2x≤1,令sin2x=t,
∴sin2x+
=t+
,则令f(t)=t+
,t∈[0,1],根据其图象可知,当x>
时,f(t)为递增的,当0<x≤
时,f(t)为递减的,
∵t∈[0,1],
∴f(t)≥f(1)=1+2=3,
∴sin2x+
≥3
∵a<sin2x+
恒成立时,只要a小于sin2x+
的最小值即可,
a<3故②对
对于③当a=1,b=-1时,虽然有a+b=0,但f(x)不是奇函数,故③错,
故选B.
对于②∵0≤sin2x≤1,令sin2x=t,
∴sin2x+
| 2 |
| sin2x |
| 2 |
| t |
| 2 |
| t |
| 2 |
| 2 |
∵t∈[0,1],
∴f(t)≥f(1)=1+2=3,
∴sin2x+
| 2 |
| sin2x |
∵a<sin2x+
| 2 |
| sin2x |
| 2 |
| sin2x |
a<3故②对
对于③当a=1,b=-1时,虽然有a+b=0,但f(x)不是奇函数,故③错,
故选B.
点评:本题考查含量词的命题的否定、不等式恒成立问题,考查的知识点比较多.

练习册系列答案
相关题目
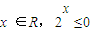 ”的否定是“对任意的
”的否定是“对任意的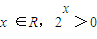 ”;
”;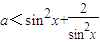 恒成立,则a的取值范围是a<3;
恒成立,则a的取值范围是a<3;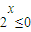 ”的否定是
”的否定是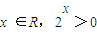 ”;
”;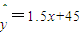 ,x∈{1,5,7,13,19},则
,x∈{1,5,7,13,19},则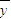 =58.5;
=58.5;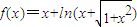 ,则对于任意实数a和b,a+b<0是f(a)+f(b))<0的充要条件;
,则对于任意实数a和b,a+b<0是f(a)+f(b))<0的充要条件;