题目内容
(本题满分14分)一个袋中装有大小和质地都相同的10个球,其中黑球4个,白球5个,红球1个。
(1)从袋中任意摸出3个球,记得到白球的个数为X,求随机变量X的概率分布和数学期望E(X);
(2)每次从袋中随机地摸出一球,记下颜色后放回.求3次摸球后,摸到黑球的次数大于摸到白球的次数的概率。
(1)分布列是:
0 1 2 3 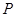
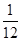
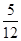
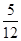
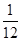
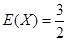
(2)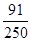
解析试题分析:(1)由题意知随机变量X的取值为0,1,2,3,所以分布列是
0 1 2 3 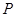
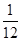
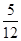
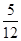
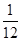
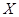 的数学期望是
的数学期望是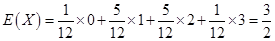 . -----7分
. -----7分
(2)记3次摸球中,摸到黑球次数大于摸到白球次数为事件A,
则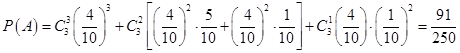
答:摸到黑球的次数大于摸到白球的次数的概率为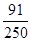 . -----14分
. -----14分
考点:本小题主要考查离散型随机变量及其分布列、数学期望、n次独立重复试验的概率的计算,考查学生的逻辑推理能力,理解问题、分析问题、解决问题的能力及分类讨论思想的应用.
点评:解决此类问题要注意判准事件的性质,根据事件的性质识别概率模型,能否正确列出
分布列将直接影响数学期望的求解.求解过程中要注意概率表示方法的一致性,题目中用小
数表示的都是小数,用分数表示的都是分数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(本小题满分10分)某网站欲调查网民对当前网页的满意程度,在登录的所有网民中,收回有效帖子共50000份,其中持各种态度的份数如下表所示.
| 很满意 | 满意 | 一般 | 不满意 |
| 10800 | 12400 | 15600 | 11200 |
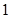 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响. 局结束,且乙比甲多得
局结束,且乙比甲多得 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好,已知某厂执行标准
,产品的等级系数越大表明产品的质量越好,已知某厂执行标准 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下: 的为一等品,等级系数
的为一等品,等级系数 的为二等品,等级系数
的为二等品,等级系数 的为三等品,
的为三等品, ,从该厂生产的产品中任取一件,其利润记为
,从该厂生产的产品中任取一件,其利润记为 ,用这个样本的频率分布估计总体分布,将频率视为概率,求
,用这个样本的频率分布估计总体分布,将频率视为概率,求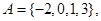 在平面直角坐标系中,点
在平面直角坐标系中,点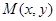 的横、纵坐标满足
的横、纵坐标满足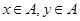 。
。 的所有坐标;
的所有坐标; 轴上的概率;
轴上的概率; 上的概率。
上的概率。 .
. ,求
,求
 ,求随机变量
,求随机变量