Question

已知圆的方程是x²+y²=2,直线y=x+b,当b为何值时,圆与直线有两个公共点,只有一个公共点,没有公共点.

Answer 1

解法一:若直线l:y=x+b和圆x²+y²=2有两个公共点,只有一个公共点,没有公共点,

则方程组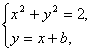有两个不同解,有两个相同解,没有实数解.

方程组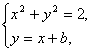消去y,得2x²+2bx+b²-2=0.

所以Δ=(2b)²-4×2(b²-2)=16-4b².

所以当Δ=16-4b²＞0,即-2＜b＜2时,圆与直线有两个公共点;

当Δ=16-4b²=0,即b=±2时,圆与直线只有一个公共点;

当Δ=16-4b²＜0,即b＞2或b＜-2时,圆与直线没有公共点.

解法二:圆x²+y²=2的圆心C的坐标为(0,0),半径长为,圆心C到直线l:y=x+b的距离d=.

当d＞r时,即＞,即|b|＞2,即b＞2或b＜-2时,圆与直线没有公共点;

当d=r时,即=,即|b|=2,即b=±2时,圆与直线只有一个公共点;

当d＜r时,即＜,即|b|＜2,即-2＜b＜2时,圆与直线有两个公共点.

点评:由于圆的特殊性判断圆与直线的位置关系,多采用判断圆心到直线的距离与半径的大小之间的关系;而以后我们将要学习的圆锥曲线与直线位置关系的判断,则需要利用方程组解的个数来判断.