题目内容
若
，
是两个非零向量，且|
|=|
|=λ|
+
|，λ∈[
，1]，则
与
-
的夹角的取值范围是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| ||
| 3 |
| b |
| a |
| b |
分析：利用菱形和向量的平行四边形法则先求出：当λ=1时，与当λ=
时，
与
-
的夹角的取值范围，即可得出．
| ||
| 3 |
| b |
| a |
| b |
解答：解：如图所示，
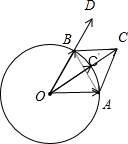
①当λ=1时，∵|
|=|
|=|
+
|，
设
=
，
=
，以OA，OB为邻边作平行四边形OACB．
则点A，B，C都在以点O为圆心，|
|为半径的圆上．
∴△OAC是等边三角形，∴∠OBA=
，
∴∠DBA=
，
∵
=
-
，∴
与
-
的夹角为
．
②当λ=
时，设|
|=x，在△OAC中，cos∠AOC=
=
，∴∠AOC=
，∴∠AOB=
．
∴∠DBA=
．
③当λ∈(
，1)时，∠DBA∈(
，
)．
综上可知：
与
-
的夹角的取值范围是[
，
]．
故选A．
①当λ=1时，∵|
| a |
| b |
| a |
| b |
设
| OA |
| a |
| OB |
| b |
则点A，B，C都在以点O为圆心，|
| a |
∴△OAC是等边三角形，∴∠OBA=
| π |
| 6 |
∴∠DBA=
| 5π |
| 6 |
∵
| BA |
| a |
| b |
| b |
| a |
| b |
| 5π |
| 6 |
②当λ=
| ||
| 3 |
| a |
| ||||
|
|
| ||
| 2 |
| π |
| 6 |
| π |
| 3 |
∴∠DBA=
| 2π |
| 3 |
③当λ∈(
| ||
| 3 |
| 2π |
| 3 |
| 5π |
| 6 |
综上可知：
| b |
| a |
| b |
| 2π |
| 3 |
| 5π |
| 6 |
故选A．
点评：本题考查了向量的运算法则、菱形的性质、数形结合等基础知识与基本技能方法，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
、
满足|
|＞|
|,且
与
同向，则
＞
与
满足
+
=0，则
∥
，
满足|
，则