题目内容
已知函数f(x)=lnx+x2+mx.
(Ⅰ)当m=-3时,求函数f(x)的极值;
(Ⅱ)若函数f(x)在定义域内为增函数,求实数m的取值范围;
(Ⅲ)若m=-1,△ABC的三个顶点A(x1,y1),B(x2,y2),C(x3,y3)在函数f(x)的图象上,且x1<x2<x3,a、b、c分别为△ABC的内角A、B、C所对的边.求证:a2+c2<b2.
(Ⅰ)当m=-3时,求函数f(x)的极值;
(Ⅱ)若函数f(x)在定义域内为增函数,求实数m的取值范围;
(Ⅲ)若m=-1,△ABC的三个顶点A(x1,y1),B(x2,y2),C(x3,y3)在函数f(x)的图象上,且x1<x2<x3,a、b、c分别为△ABC的内角A、B、C所对的边.求证:a2+c2<b2.
分析:(Ⅰ)对f(x)求导,令f,(x)=0,解得x的值;由f'(x)与f(x)随x的变化情况求出f(x)的极值;
(Ⅱ)f(x)在定义域内为增函数时,f,(x)≥0恒成立,求出m的取值范围;
(Ⅲ)由(Ⅱ)知m=-1时,f(x)为定义域上的增函数,△ABC的顶点在f(x)的图象上,由两点间的距离公式求出a2,c2,b2,即得所证.
(Ⅱ)f(x)在定义域内为增函数时,f,(x)≥0恒成立,求出m的取值范围;
(Ⅲ)由(Ⅱ)知m=-1时,f(x)为定义域上的增函数,△ABC的顶点在f(x)的图象上,由两点间的距离公式求出a2,c2,b2,即得所证.
解答:解:(Ⅰ)∵f(x)=lnx+x2+mx,定义域为(0,+∞),
∴f,(x)=
+2x+m;
当m=-3时,f,(x)=
+2x+3,
令f,(x)=0,∴
=0,即
=0,解得x=
或x=1;
则f'(x),f(x)随x的变化情况如下表:
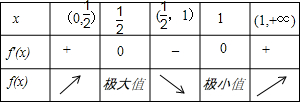
∴f(x)极大值=f(
)=-ln2-
,f(x)极小值=f(1)=-2;
(Ⅱ)函数f(x)在定义域内为增函数,∴x>0时,f,(x)=
+2x+m≥0恒成立,
∴m≥-(
+2x)(其中x>0)恒成立;
∵x>0,∴
+2x≥2
(当且仅当x=
时取等号),
∴-(
+2x)max=-2
,∴m≥-2
;
∴实数m的取值范围是[-2
,+∞);
(Ⅲ)由(Ⅱ)知m=-1时,f(x)在(0,+∞)上为增函数,
△ABC的顶点A(x1,y1),B(x2,y2),C(x3,y3)在函数f(x)的图象上,
且x1<x2<x3,∴y1<y2<y3;
∴a2=|BC|2=(x3-x2)2+(y3-y2)2,
c2=|AB|2=(x2-x1)2+(y2-y1)2,
b2=|AC|2=(x3-x1)2+(y3-y1)2=[(x3-x2)+(x2-x1)]2+[(y3-y2)+(y2-y1)]2
=(x3-x2)2+(x2-x1)2+(y3-y2)2+(y2-y1)2+2[(x3-x2)(x2-x1)+(y3-y2)(y2-y1)];
∴a2+c2<b2
∴f,(x)=
| 1 |
| x |
当m=-3时,f,(x)=
| 1 |
| x |
令f,(x)=0,∴
| 2x2-3x+1 |
| x |
| (2x-1)(x-1) |
| x |
| 1 |
| 2 |
则f'(x),f(x)随x的变化情况如下表:

∴f(x)极大值=f(
| 1 |
| 2 |
| 5 |
| 4 |
(Ⅱ)函数f(x)在定义域内为增函数,∴x>0时,f,(x)=
| 1 |
| x |
∴m≥-(
| 1 |
| x |
∵x>0,∴
| 1 |
| x |
| 2 |
| ||
| 2 |
∴-(
| 1 |
| x |
| 2 |
| 2 |
∴实数m的取值范围是[-2
| 2 |
(Ⅲ)由(Ⅱ)知m=-1时,f(x)在(0,+∞)上为增函数,
△ABC的顶点A(x1,y1),B(x2,y2),C(x3,y3)在函数f(x)的图象上,
且x1<x2<x3,∴y1<y2<y3;
∴a2=|BC|2=(x3-x2)2+(y3-y2)2,
c2=|AB|2=(x2-x1)2+(y2-y1)2,
b2=|AC|2=(x3-x1)2+(y3-y1)2=[(x3-x2)+(x2-x1)]2+[(y3-y2)+(y2-y1)]2
=(x3-x2)2+(x2-x1)2+(y3-y2)2+(y2-y1)2+2[(x3-x2)(x2-x1)+(y3-y2)(y2-y1)];
∴a2+c2<b2
点评:本题考查了利用导数求函数的极值,函数与不等式的应用以及两点间的距离公式等知识,是较难的题.

练习册系列答案
相关题目