题目内容
【题目】某上市股票在30天内每股的交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在图中的两条线段上（如图）．该股票在30天内（包括第30天）的日交易量Q（万股）与时间t（天）的函数关系式为Q=40﹣t（0≤t≤30且t∈N）．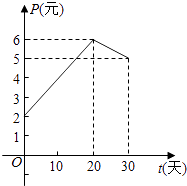 
（1）根据提供的图象，求出该种股票每股的交易价格P（元）与时间t（天）所满足的函数关系式；
（2）用y（万元）表示该股票日交易额（日交易额=日交易量×每股的交易价格），写出y关于t的函数关系式，并求出这30天中第几天日交易额最大，最大值为多少．
【答案】
（1）解：设表示前20天每股的交易价格P（元）与时间t（天）的一次函数关系式为P=k1t+m，
由图象得： 
，解得： 
，即P= 
t+2；
设表示第20天至第30天每股的交易价格P（元）与时间t（天）的一次函数关系式为P=k2t+n，
即P=﹣ 
t+8．
综上知P= 
（t∈N）
（2）解：由（1）可得y= 
．
即y= 
（t∈N）．
当0≤t＜20时，函数y=﹣ t2+6t+80的图象的对称轴为直线t=15，
∴当t=15时，ymax=125；
当20≤t≤30时，函数y= t2﹣12t+320的图象的对称轴为直线t=60，
∴该函数在[20，30]上单调递减，即当t=20时，ymax=120．
而125＞120，
∴第15天日交易额最大，最大值为125万元
【解析】（1）根据图象可知此函数为分段函数，在（0，20]和（20，30]两个区间利用待定系数法分别求出一次函数关系式联立可得P的解析式；（2）因为Q与t成一次函数关系，根据表格中的数据，取出两组即可确定出Q的解析式；根据股票日交易额=交易量×每股较易价格可知y=PQ，可得y的解析式，分别在各段上利用二次函数求最值的方法求出即可．
