题目内容
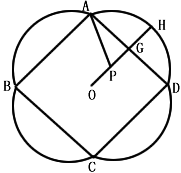
如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l, .(1)求l关于θ的函数关系式;(2)定义比值
.(1)求l关于θ的函数关系式;(2)定义比值 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足:
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足: 时,招贴画最优美.
时,招贴画最优美.
【答案】分析:(1)先对θ所在范围分情况求解,最后综合即可;
(2)先根据条件求出OP=a- ,θ∈(
,θ∈( ,
, );进而得到
);进而得到 =
= ,然后借助于两次求导求出函数的最大值点即可得到结论.
,然后借助于两次求导求出函数的最大值点即可得到结论.
解答:解:(1)当θ∈( ,
, )时,点P在线段OG上,AP=
)时,点P在线段OG上,AP= ;
;
当θ∈( ,
, )时,点P在线段GH上,AP=
)时,点P在线段GH上,AP= =
= ;
;
当θ= 时,AP=a.
时,AP=a.
综上所述AP= ,θ∈(
,θ∈( ,
, ),
),
所以,弧AD的长L=AP•2θ= .
.
故所求函数关系式为L= ,θ∈(
,θ∈( ,
, ).
).
(2)证明:当θ∈( ,
, )时,OP=OG-PG=a-
)时,OP=OG-PG=a- =a-
=a- ;
;
当θ∈( ,
, )时,OP=OG+GH=a+
)时,OP=OG+GH=a+ =a-
=a- =a-
=a- ;
;
当θ= 时,OP=a.
时,OP=a.
所以,OP=a- ,θ∈(
,θ∈( ,
, ).
).
从而, =
= ,θ∈(
,θ∈( ,
, ).
).
记f(θ)= ,θ∈(
,θ∈( ,
, ).
).
则f′(θ)=
令f′(θ)=0得θ(cosθ+sinθ)=sinθ-cosθ
因为θ∈( ,
, )所以cosθ+sinθ≠0,从而θ=
)所以cosθ+sinθ≠0,从而θ= ,
,
显然θ≠ ,所以θ=
,所以θ= =
= =tan(θ-
=tan(θ- )
)
记满足θ=tan(θ- )的θ=θ.下面证明θ是函数f(θ)的极值点.
)的θ=θ.下面证明θ是函数f(θ)的极值点.
设g(θ)=θ(cosθ+sinθ)-(sinθ-cosθ),θ∈( ,
, ),
),
则g′(θ)=θ(cosθ-sinθ)<0上θ∈( ,
, )恒成立.
)恒成立.
从而g(θ)在θ∈( ,
, )上单调递减,
)上单调递减,
所以,当θ∈( ,θ)时g(θ)>0,即f′(θ)>0,f(θ)在(
,θ)时g(θ)>0,即f′(θ)>0,f(θ)在( ,θ)上单调递增,
,θ)上单调递增,
当θ∈(θ, )时,g(θ)<0,即f′(θ)<0,f(θ)在(θ,
)时,g(θ)<0,即f′(θ)<0,f(θ)在(θ, )上单调递减.
)上单调递减.
故f(θ)在θ=θ.处取得极大值也是最大值.
所以:当θ满足θ=tan(θ- )时,函数f(θ)即
)时,函数f(θ)即 取得最大值,此时招贴画最优美.
取得最大值,此时招贴画最优美.
点评:本题主要考察解三角形在生活中的应用问题.解决本题的第二问时涉及到了两次求导来求函数的最值,难度较大.
(2)先根据条件求出OP=a-
 ,θ∈(
,θ∈( ,
, );进而得到
);进而得到 =
= ,然后借助于两次求导求出函数的最大值点即可得到结论.
,然后借助于两次求导求出函数的最大值点即可得到结论.解答:解:(1)当θ∈(
 ,
, )时,点P在线段OG上,AP=
)时,点P在线段OG上,AP= ;
;当θ∈(
 ,
, )时,点P在线段GH上,AP=
)时,点P在线段GH上,AP= =
= ;
;当θ=
 时,AP=a.
时,AP=a.综上所述AP=
 ,θ∈(
,θ∈( ,
, ),
),所以,弧AD的长L=AP•2θ=
 .
.故所求函数关系式为L=
 ,θ∈(
,θ∈( ,
, ).
).(2)证明:当θ∈(
 ,
, )时,OP=OG-PG=a-
)时,OP=OG-PG=a- =a-
=a- ;
;当θ∈(
 ,
, )时,OP=OG+GH=a+
)时,OP=OG+GH=a+ =a-
=a- =a-
=a- ;
;当θ=
 时,OP=a.
时,OP=a.所以,OP=a-
 ,θ∈(
,θ∈( ,
, ).
).从而,
 =
= ,θ∈(
,θ∈( ,
, ).
).记f(θ)=
 ,θ∈(
,θ∈( ,
, ).
).则f′(θ)=

令f′(θ)=0得θ(cosθ+sinθ)=sinθ-cosθ
因为θ∈(
 ,
, )所以cosθ+sinθ≠0,从而θ=
)所以cosθ+sinθ≠0,从而θ= ,
,显然θ≠
 ,所以θ=
,所以θ= =
= =tan(θ-
=tan(θ- )
)记满足θ=tan(θ-
 )的θ=θ.下面证明θ是函数f(θ)的极值点.
)的θ=θ.下面证明θ是函数f(θ)的极值点.设g(θ)=θ(cosθ+sinθ)-(sinθ-cosθ),θ∈(
 ,
, ),
),则g′(θ)=θ(cosθ-sinθ)<0上θ∈(
 ,
, )恒成立.
)恒成立.从而g(θ)在θ∈(
 ,
, )上单调递减,
)上单调递减,所以,当θ∈(
 ,θ)时g(θ)>0,即f′(θ)>0,f(θ)在(
,θ)时g(θ)>0,即f′(θ)>0,f(θ)在( ,θ)上单调递增,
,θ)上单调递增,当θ∈(θ,
 )时,g(θ)<0,即f′(θ)<0,f(θ)在(θ,
)时,g(θ)<0,即f′(θ)<0,f(θ)在(θ, )上单调递减.
)上单调递减.故f(θ)在θ=θ.处取得极大值也是最大值.
所以:当θ满足θ=tan(θ-
 )时,函数f(θ)即
)时,函数f(θ)即 取得最大值,此时招贴画最优美.
取得最大值,此时招贴画最优美.点评:本题主要考察解三角形在生活中的应用问题.解决本题的第二问时涉及到了两次求导来求函数的最值,难度较大.

练习册系列答案
相关题目
 如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,
如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,

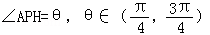 .
.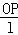 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足:
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足: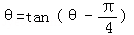 时,招贴画最优美.
时,招贴画最优美.