题目内容
设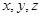
为正实数，满足
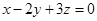，则
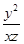的最小值是 ．
3
解析试题分析：由已知得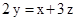
，∵
，∴
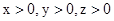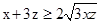，即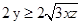
，两边同时平方得，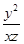
.
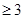考点：1、不等式的性质；2、基本不等式.
练习册系列答案
相关题目
，则
的最小值为 .
若不等式
≥
对任意实数
恒成立，则
的取值集合是________________.
对一切实数
恒成立，则实数
的取值范围是 ．
则
________________________。
均为正数，且
，
，
.
，
.
的最小值；
.设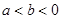
，则下列不等式中
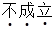的是（ ）
A． | B． |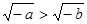
C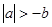． | D． |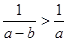
题目内容
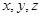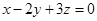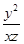设为正实数，满足，则的最小值是 ．
3
解析试题分析：由已知得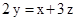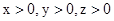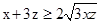，∵，∴，即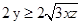，两边同时平方得，.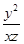
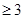考点：1、不等式的性质；2、基本不等式.
设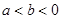 ，则下列不等式中的是（ ）
| A． | B． |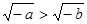
| C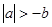． | D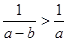． |