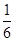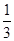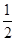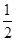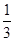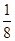题目内容
一个暗箱里放着6个黑球、4个白球.(每个球的大小和质量均相同)
(1)不放回地依次取出2个球,若第1次取出的是白球,求第2次取到黑球的概率;
(2)有放回地依次取出2个球,求两球颜色不同的概率;
(3)有放回地依次取出3个球,求至少取到两个白球的概率.
(1)不放回地依次取出2个球,若第1次取出的是白球,求第2次取到黑球的概率;
(2)有放回地依次取出2个球,求两球颜色不同的概率;
(3)有放回地依次取出3个球,求至少取到两个白球的概率.
(1) 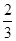 ;(2)
;(2)  ;(3)
;(3)  。
。
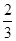 ;(2)
;(2)  ;(3)
;(3)  。
。本试题主要是考查了古典概型概率的求解和独立事件的概率,以及二项分布的运用。
(1)首先第一问中是不放回的取出2个球,那么暗箱里放着6个黑球、4个白球,所有的情况为
而第1次取出的是白球,求第2次取到黑球的情况有 ,利用概率公式求解得到。
,利用概率公式求解得到。
(2)因为有放回地依次取出2个球,那么每次有10个球,那么取到黑球的概率为3/5,白球的概率为2/5,那么利用独立事件概率乘法公式得到
(3)利用因为有放回地依次取出3个球,求至少取到两个白球的概率,运用n此独立重复试验中事件发生k次的概率公式解得。
解:(1)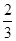 4分
4分
(2) 8分
8分
(3) 13分
13分
(1)首先第一问中是不放回的取出2个球,那么暗箱里放着6个黑球、4个白球,所有的情况为

而第1次取出的是白球,求第2次取到黑球的情况有
 ,利用概率公式求解得到。
,利用概率公式求解得到。(2)因为有放回地依次取出2个球,那么每次有10个球,那么取到黑球的概率为3/5,白球的概率为2/5,那么利用独立事件概率乘法公式得到
(3)利用因为有放回地依次取出3个球,求至少取到两个白球的概率,运用n此独立重复试验中事件发生k次的概率公式解得。
解:(1)
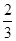 4分
4分(2)
 8分
8分(3)
 13分
13分
练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 与向量
与向量 垂直的概率是( )
垂直的概率是( )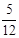
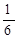


 ,
,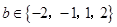 .
. 与圆
与圆 有公共点的概率.
有公共点的概率.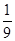
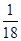
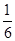

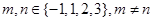 ,则方程
,则方程 表示的曲线是焦点在x轴上的双曲线概率为
表示的曲线是焦点在x轴上的双曲线概率为 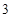 的倍数的概率是
的倍数的概率是