题目内容
 (2012•西城区二模)如图,四棱锥E-ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
(2012•西城区二模)如图,四棱锥E-ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.(Ⅰ)求证:AB⊥ED;
(Ⅱ)线段EA上是否存在点F,使DF∥平面BCE?若存在,求出
| EF | EA |
分析:(Ⅰ)取AB中点O,连接EO,DO,则EO⊥AB,证明四边形OBCD为矩形,可得AB⊥DO,从而可得AB⊥平面EOD,由此即可证得结论;
(Ⅱ)F为EA中点时,有DF∥平面BCE,取EB中点G,连接CG,FG,证明DF∥CG,利用线面平行的判定可得DF∥平面BCE.
(Ⅱ)F为EA中点时,有DF∥平面BCE,取EB中点G,连接CG,FG,证明DF∥CG,利用线面平行的判定可得DF∥平面BCE.
解答: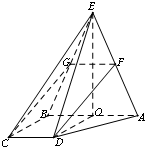 (Ⅰ)证明:取AB中点O,连接EO,DO.
(Ⅰ)证明:取AB中点O,连接EO,DO.
因为EA=EB,所以EO⊥AB. …(2分)
因为AB∥CD,AB=2CD,
所以BO∥CD,BO=CD.
又因为AB⊥BC,所以四边形OBCD为矩形,
所以AB⊥DO. …(4分)
因为EO∩DO=O,所以AB⊥平面EOD. …(5分)
所以AB⊥ED. …(6分)
(Ⅱ)解:点F满足
=
,即F为EA中点时,有DF∥平面BCE.…(7分)
证明如下:取EB中点G,连接CG,FG. …(8分)
因为F为EA中点,所以FG∥AB,FG=
AB.
因为AB∥CD,CD=
AB,所以FG∥CD,FG=CD.
所以四边形CDFG是平行四边形,所以DF∥CG. …(11分)
因为DF?平面BCE,CG?平面BCE,…(12分)
所以DF∥平面BCE. …(13分)
 (Ⅰ)证明:取AB中点O,连接EO,DO.
(Ⅰ)证明:取AB中点O,连接EO,DO.因为EA=EB,所以EO⊥AB. …(2分)
因为AB∥CD,AB=2CD,
所以BO∥CD,BO=CD.
又因为AB⊥BC,所以四边形OBCD为矩形,
所以AB⊥DO. …(4分)
因为EO∩DO=O,所以AB⊥平面EOD. …(5分)
所以AB⊥ED. …(6分)
(Ⅱ)解:点F满足
| EF |
| EA |
| 1 |
| 2 |
证明如下:取EB中点G,连接CG,FG. …(8分)
因为F为EA中点,所以FG∥AB,FG=
| 1 |
| 2 |
因为AB∥CD,CD=
| 1 |
| 2 |
所以四边形CDFG是平行四边形,所以DF∥CG. …(11分)
因为DF?平面BCE,CG?平面BCE,…(12分)
所以DF∥平面BCE. …(13分)
点评:本题考查线面垂直,考查线面平行,掌握线面垂直、线面平行的判定方法是关键.

练习册系列答案
相关题目
 (2012•西城区二模)如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.
(2012•西城区二模)如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB. (2012•西城区二模)执行如图所示的程序框图,若输入如下四个函数:
(2012•西城区二模)执行如图所示的程序框图,若输入如下四个函数: