题目内容
【题目】如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点. 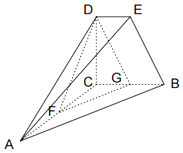
(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值.
【答案】
(1)证明:∵F、G分别是AC、BC中点.
∴FG∥AB,
∵FG平面ABE,AB平面ABE,
∴FG∥平面ABE,
∵DE∥BC,BC=2DE,G是BC中点,
∴DE ![]() BG,∴四边形DEBG是平行四边形,
BG,∴四边形DEBG是平行四边形,
∴DG∥BE,
∵DG平面ABE,BE平面ABE,
∴DG∥平面ABE,
∵DG∩FG=G,DG,FG平面DFG,
AB∩BE=B,AB,BE平面ABE,
∴平面DFG∥平面ABE
(2)解:∵DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
∴以C为原点,CA为x轴,以CB为y轴,以CD为z轴,建立空间直角坐标系,

∵AC=2BC=2CD=4,
∴A(4,0,0),B(0,2,0),C(0,0,2),E(0,1,2),
![]() =(﹣4,1,2),
=(﹣4,1,2), ![]() =(﹣4,2,0),
=(﹣4,2,0), ![]() =(﹣4,0,2),
=(﹣4,0,2),
设平面ABE的法向量 ![]() =(x,y,z),
=(x,y,z),
则 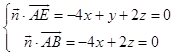 ,取x=1,得
,取x=1,得 ![]() =(1,0,2),
=(1,0,2),
平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
则cos< ![]() >=
>= ![]() .
.
∴二面角E﹣AB﹣C的余弦值为cosα= ![]() ,
,
则sinα= ![]() ,tanα=
,tanα= ![]() =
= ![]() .
.
∴二面角E﹣AB﹣C的正切值为 ![]() .
.
【解析】(1)推导出FG∥AB,从而FG∥平面ABE,从而出四边形DEBG是平行四边形,从而DG∥BE,进而DG∥平面ABE,由此能证明平面DFG∥平面ABE.(2)以C为原点,CA为x轴,以CB为y轴,以CD为z轴,建立空间直角坐标系,利用向量法能求出二面角E﹣AB﹣C的正切值.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案