题目内容
【题目】若
是一个集合，
是一个以的某些子集为元素的集合，且满足：（1）属于，
属于；（2）中任意多个元素的并集属于；（3）中任意多个元素的交集属于，则称是集合上的一个拓补.已知集合
，对于下面给出的四个集合：
①
②
③
④
其中是集合上的拓补的集合的序号是______.（写出所有的拓补的集合的序号）
【答案】②
【解析】
根据集合
上的拓补的集合
的定义，逐个验证即可.
对于①：
，而
，故①不是集合上的拓补的集合；
对于②：
，满足：（1）属于，
属于；（2）中任意多个元素的并集属于；（3）中任意多个元素的交集属于，故②是集合上的拓补的集合；
对于③：
，而
，故③不是集合上的拓补的集合；
对于④：
，满足：（1）属于，属于；（2）中任意多个元素的并集属于；但
不满足（3）中任意多个元素的交集属于，故④不是集合上的拓补的集合.
故答案为：②.
【题目】2019年10月18日-27日，第七届世界军人运动会在湖北武汉举办，中国代表团共获得133金64银42铜，共239枚奖牌.为了调查各国参赛人员对主办方的满意程度，研究人员随机抽取了500名参赛运动员进行调查，所得数据如下所示，现有如下说法：①在参与调查的500名运动员中任取1人，抽到对主办方表示满意的男性运动员的概率为
；②在犯错误的概率不超过1%的前提下可以认为“是否对主办方表示满意与运动员的性别有关”；③没有99.9%的把握认为“是否对主办方表示满意与运动员的性别有关”；则正确命题的个数为（ ）附：
男性运动员 | 女性运动员 | |||||
对主办方表示满意 | 200 | 220 | ||||
对主办方表示不满意 | 50 | 30 | ||||
| 0.100 | 0.050 | 0.010 | 0.001 | ||
k | 2.706 | 3.841 | 6.635 | 10.828 | ||
A.0B.1C.2D.3
【题目】蚂蚁森林是支付宝客户端为首期“碳账户”设计的一款公益行动：用户通过步行、地铁出行、在线缴纳水电煤气费、网络挂号、网络购票等行为就会减少相应的碳排放量，可以用来在支付宝里养一棵虚拟的树.这棵树长大后，公益组织、环保企业等蚂蚁生态伙伴们可以在现实沙漠化地区（阿拉善、通辽、库布齐等）种下一棵实体的树目前通辽地区对部分基地樟子松幼苗的培育技术进行了改进，为了了解改进后的效果，现从改进前后的树苗培育基地各抽取了
株产品作为样本，检测其同样生长周期的高度（单位：
），若高度不低于
才适合移植，否则继续等待生长图1是改进前的样本的频率分布直方图，表2是改进后的样本频率分布表.
图1
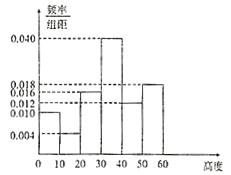
表2技术改进后样本的频率分布表
高度 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
（1）根据图1和表2提供的信息，试从移植率的角度对培育技术改进前后的优劣进行比较；
（2）估计培育技术未改进的基地树苗高度的平均数；
（3）在市场中，规定高度在
内的为三等苗，
内的为二等苗，
内的为一等苗.现从表2高度不低于
的树苗样本中采用分层抽样的方法抽取
株，再从这株幼苗中随机抽取
株，求这株中一、二、三等苗都有的概率.
