题目内容
已知点p是圆(x+1)2+y2=16上的动点,圆心为B.A(1,0)是圆内的定点;PA的中垂线交BP于点Q.
(1)求点Q的轨迹C的方程;
(2)若直线l交轨迹C于M,N(MN与x轴、y轴都不平行)两点,G为MN的中点,求KMN•KOG的值(O为坐标系原点).
(1)求点Q的轨迹C的方程;
(2)若直线l交轨迹C于M,N(MN与x轴、y轴都不平行)两点,G为MN的中点,求KMN•KOG的值(O为坐标系原点).
(1)由条件知:|QA|=|QP|,
∵|QB|+|QP|=4,
∴|QB|+|QA|=4,
∵|AB|=2<4,
所以点Q的轨迹是以B,A为焦点的椭圆,
∵2a=4,2c=2,∴b2=3,
所以点Q的轨迹C的方程是
+
=1.
(2)设M(x1,y1),N(x2,y2)(x1≠x2,y1≠y2),则G(
,
).
∵直线l与椭圆相较于点M,N,
∴
+
=1,
+
=1,
∴
+
=0,可得
=-
.
∵kMN=
,kOG=
,
∴kMN×kOG=
=-
.
另设M(x1,y1),N(x2,y2)(x1≠x2,y1≠y2),直线MN的方程为y=kx+b(k≠0),
则G(
,
),
∵y1=kx1+b,y2=kx2+b,∴y1+y2=k(x1+x2)+2b,
∴kOG=
=k+
,
将y=kx+b代入椭圆方程得:(4k2+3)x2+8kbx+4b2-12=0,
∴x1+x2=-
,
∴kOG=k+
=k-
=-
,
所以kMN•kOG=k•(-
)=-
.
∵|QB|+|QP|=4,
∴|QB|+|QA|=4,
∵|AB|=2<4,
所以点Q的轨迹是以B,A为焦点的椭圆,
∵2a=4,2c=2,∴b2=3,
所以点Q的轨迹C的方程是
| x2 |
| 4 |
| y2 |
| 3 |
(2)设M(x1,y1),N(x2,y2)(x1≠x2,y1≠y2),则G(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
∵直线l与椭圆相较于点M,N,
∴
| ||
| 4 |
| ||
| 3 |
| ||
| 4 |
| ||
| 3 |
∴
| ||||
| 4 |
| ||||
| 3 |
| ||||
|
| 3 |
| 4 |
∵kMN=
| y1-y2 |
| x1-x2 |
| y1+y2 |
| x1+x2 |
∴kMN×kOG=
| ||||
|
| 3 |
| 4 |
另设M(x1,y1),N(x2,y2)(x1≠x2,y1≠y2),直线MN的方程为y=kx+b(k≠0),
则G(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
∵y1=kx1+b,y2=kx2+b,∴y1+y2=k(x1+x2)+2b,
∴kOG=
| y1+y2 |
| x1+x2 |
| 2b |
| x1+x2 |
将y=kx+b代入椭圆方程得:(4k2+3)x2+8kbx+4b2-12=0,
∴x1+x2=-
| 8kb |
| 4k2+3 |
∴kOG=k+
| 2b | ||
|
| 4k2+3 |
| 4k |
| 3 |
| 4k |
所以kMN•kOG=k•(-
| 3 |
| 4k |
| 3 |
| 4 |

练习册系列答案
相关题目
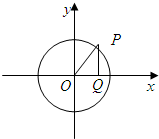 已知点P是圆x2+y2=1上的一个动点,过点P作PQ⊥x轴于点Q,设
已知点P是圆x2+y2=1上的一个动点,过点P作PQ⊥x轴于点Q,设