题目内容
已知点P是圆x2+y2=1上的一个动点，过点P作PQ⊥x轴于点Q，设| OM |
| OP |
| OQ |
分析：设点P（m，n），由题意得 Q（m，0 ），m2+n2=1 ①，设点 M（x，y ），由向量间的关系得到m=
，且 n=y，代入①式化简可得所求．
| x |
| 2 |
解答：解：设点P（m，n），由题意得 Q（m，0 ），m2+n2=1 ①，
设点 M（x，y ）．
∵
=
+
，∴（ x，y ）=（m，n）+（m，0 ）=（2m，n ），
∴x=2m，y=n，即 m=
，且 n=y ②．
把②代入①得
+y2=1，
故答案为
+y2=1．
设点 M（x，y ）．
∵
| OM |
| OP |
| OQ |
∴x=2m，y=n，即 m=
| x |
| 2 |
把②代入①得
| x2 |
| 4 |
故答案为
| x2 |
| 4 |
点评：本题考查用代入法求轨迹方程的方法，建立点 M的坐标（x，y ）和点P的坐标（m，n）之间的关系，是解题的关键．
练习册系列答案
相关题目
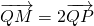的点M的轨迹为曲线C．
的点M的轨迹为曲线C．