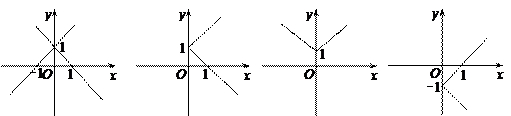题目内容
若不等式x2+ax+1≥0对于一切x∈成立,则a的取值范围是( )
| A.(0,+∞) | B.[-2,+∞) |
| C. | D.(-3,+∞) |
C
解析

练习册系列答案
相关题目
设函数f(x)是定义在R上的奇函数,且当x≥0时,f(x)是单调递减,若数列{an}是等差数列,且a3<0,则f(a1)+f(a2)+f(a3)+f(a4)+f(a5)的值
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)-g(x)=ex,则有( )
| A.f(2)<f(3)<g(0) | B.g(0)<f(3)<f(2) |
| C.f(2)<g(0)<f(3) | D.g(0)<f(2)<f(3) |
设x>0且ax<bx<1,a,b∈(0,+∞),则a、b的大小关系是( )
| A.b<a<1 | B.a<b<1 |
| C.1<b<a | D.1<a<b |
设函数f(x)=-x2+4x在[m,n]上的值域是[-5,4],则m+n的取值所组成的集合为
( )
| A.[0,6] | B.[-1,1] |
| C.[1,5] | D.[1,7] |
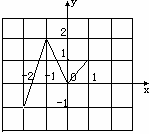
设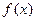 是定义在R上的周期为3的周期函数,如图表示该函数在区间
是定义在R上的周期为3的周期函数,如图表示该函数在区间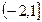 上的图像,则
上的图像,则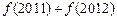 =
=
| A.3 | B.2 | C.1 | D.0 |
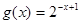 在同一直角坐标系下的图象大致是( )
在同一直角坐标系下的图象大致是( )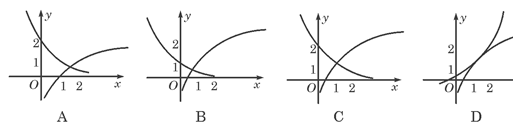 [来源:学+科+网]
[来源:学+科+网]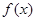 是定义在
是定义在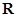 上的偶函数,且当
上的偶函数,且当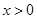 时,
时,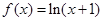 ,则函数
,则函数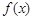 的大致图像为
的大致图像为