题目内容
若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)-g(x)=ex,则有( )
| A.f(2)<f(3)<g(0) | B.g(0)<f(3)<f(2) |
| C.f(2)<g(0)<f(3) | D.g(0)<f(2)<f(3) |
D
解析考点:函数奇偶性的性质.
分析:因为函数f(x),g(x)分别是R上的奇函数、偶函数,所以f(-x)=-f(x),g(-x)=g(x).
用-x代换x得:f(-x)-g(-x)=-f(x)-g(x)=e-x,又由f(x)-g(x)=ex联立方程组,可求出f(x),g(x)的解析式进而得到答案.
解:用-x代换x得:f(-x)-g(-x)=e-x,即f(x)+g(x)=-e-x,
又∵f(x)-g(x)=ex
∴解得:f(x)=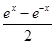 ,g(x)="-"
,g(x)="-" 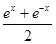 ,
,
故f(x)单调递增,又f(0)=0,g(0)=-1,有g(0)<f(2)<f(3)
故选D.

练习册系列答案
相关题目
若函数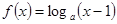
 的图像恒过定点,则定点的坐标为 ( )
的图像恒过定点,则定点的坐标为 ( )
A.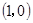 | B.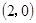 | C.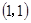 | D.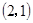 |
.函数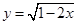 的定义域为集合
的定义域为集合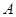 ,函数
,函数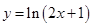 的定义域为集合
的定义域为集合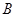 ,则
,则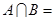
A.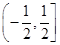 | B.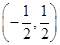 | C.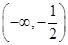 | D.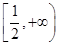 |
利用计算器,列出自变量和函数值的对应值如下表:
| x | 0.2 | 0.6 | 1.0 | 1.4 | 1.8 |
| y=2x | 1.149 | 1.516 | 2.0 | 2.639 | 3.482 |
| y=x2 | 0.04 | 0.36 | 1.0 | 1.96 | 3.24 |
| | | | | | |
| x | 2.2 | 2.6 | 3.0 | 3.4 | … |
| y=2x | 4.595 | 6.063 | 8.0 | 10.556 | … |
| y=x2 | 4.84 | 6.76 | 9.0 | 11.56 | … |
| A.(0.6,1.0) | B.(1.4,1.8) |
| C.(1.8,2.2) | D.(2.6,3.0) |
若不等式x2+ax+1≥0对于一切x∈成立,则a的取值范围是( )
| A.(0,+∞) | B.[-2,+∞) |
| C. | D.(-3,+∞) |
若关于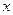 的方程
的方程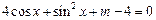 恒有实数解,则实数m的取值范围是( )
恒有实数解,则实数m的取值范围是( )
| A.[0,5] | B.[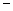 1,8] 1,8] | C.[0,8] | D.[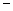 1,+∞) 1,+∞) |
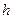 随时间
随时间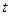 变化的图象可能是( )
变化的图象可能是( )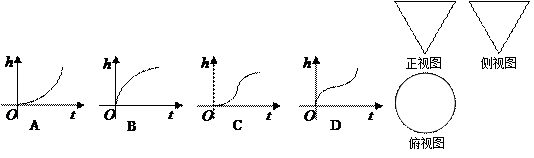
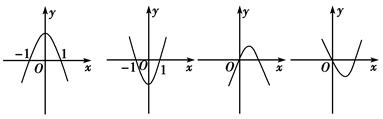
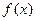 对任意的
对任意的
 有
有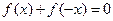 ,且当
,且当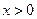 时,
时, ,则函数
,则函数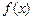 的大致图像为
的大致图像为
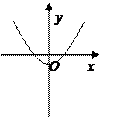
 (A) (B)
(A) (B)