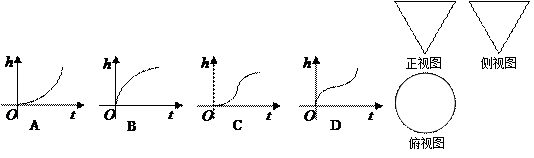题目内容
设函数f(x)是定义在R上的奇函数,且当x≥0时,f(x)是单调递减,若数列{an}是等差数列,且a3<0,则f(a1)+f(a2)+f(a3)+f(a4)+f(a5)的值
| A.恒为正数 | B.恒为负数 | C.恒为0 | D.可正可负 |
A
解析由题设知a2+a4=2a3<0,a1+a5=2a3<0,x≥0,f(x)单调递减,所以在R上,f(x)都单调递减,因为f(0)=0,所以x≥0时,f(x)<0,x<0时,f(x)>0,由此能够导出f(a1)+f(a2)+f(a3)+f(a4)+f(a5)的值恒为正数
解:∵函数f(x)是定义在R上的奇函数,
且当x≥0时,f(x)单调递减,
数列{an}是等差数列,且a3<0,
∴a2+a4=2a3<0,
a1+a5=2a3<0,
x≥0,f(x)单调递减,
所以在R上,f(x)都单调递减,
因为f(0)=0,
所以x≥0时,
f(x)<0,x<0时,f(x)>0,
∴f(a3)>0
∴f(a1)+f(a5)>0,
∴f(a2)+f(a4)>0.
故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
.已知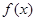 为偶函数,且
为偶函数,且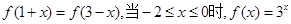 ,
,
若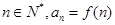 ,则
,则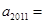 ( )
( )
A.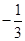 | B.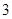 | C.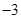 | D.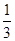 |
若函数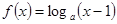
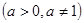 的图像恒过定点,则定点的坐标为 ( )
的图像恒过定点,则定点的坐标为 ( )
A.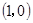 | B.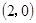 | C.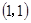 | D.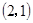 |
若函数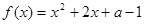 没有零点,则实数
没有零点,则实数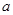 的取值范围为( )
的取值范围为( )
A.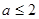 | B.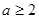 | C.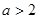 | D.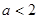 |
若不等式x2+ax+1≥0对于一切x∈成立,则a的取值范围是( )
| A.(0,+∞) | B.[-2,+∞) |
| C. | D.(-3,+∞) |
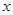 的方程
的方程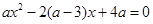 有两个负实根,则整数
有两个负实根,则整数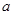 的取值集合
的取值集合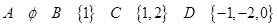
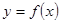 ,则下图(2)中的图像对应的函
,则下图(2)中的图像对应的函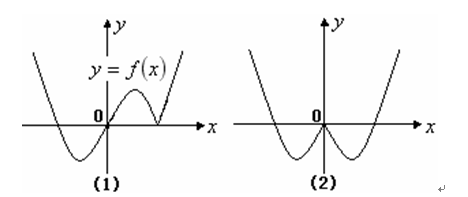
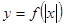
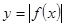
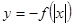
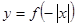
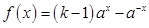
 为奇函数,且为增函数, 则函
为奇函数,且为增函数, 则函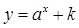 的图象为 ( )
的图象为 ( )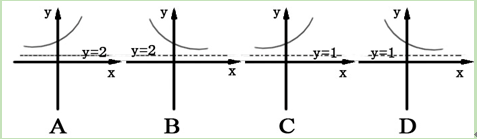
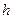 随时间
随时间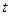 变化的图象可能是( )
变化的图象可能是( )