题目内容
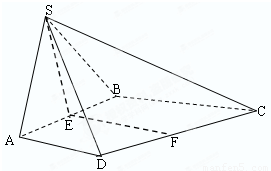
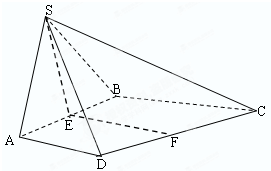 如图,等边△SAB与直角梯形ABCD垂直,AD⊥AB,BC⊥AB,AB=BC=2,AD=1.若E,F分别为AB,CD的中点.
如图,等边△SAB与直角梯形ABCD垂直,AD⊥AB,BC⊥AB,AB=BC=2,AD=1.若E,F分别为AB,CD的中点.(1)求|
| SC |
| SD |
(2)求面SCD与面SAB所成的二面角大小.
分析:(1)连接SF,证明SE⊥面ABCD,可得SE⊥EF,利用|
+
|=2|
,即可求得结论;
(2)建立直角坐标系,分别求出面SCD与面SAB的法向量,利用向量的夹角公式,即可求面SCD与面SAB所成的二面角大小.
| SC |
| SD |
| SF| |
(2)建立直角坐标系,分别求出面SCD与面SAB的法向量,利用向量的夹角公式,即可求面SCD与面SAB所成的二面角大小.
解答:解:(1)连接SF,则
在正△SAB中,AB=2,SE=
,E为AB的中点,∴SE=
,SE⊥AB
∵BC=2,AD=1,E,F分别为AB,CD的中点,∴EF=
∵等边△SAB与直角梯形ABCD垂直,SE⊥AB
∴SE⊥面ABCD,∴SE⊥EF
直角△SEF中,|SF|=
=
,
∴|
+
|=2|
=
;
(2)建立如图所示的直角坐标系,
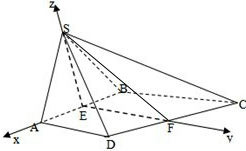
则S(0,0,
),D(1,1,0),C(-1,2,0)
设面SCD的法向量为
=(x,y,z),则由
,可得
取x=1,可得
=(1,2,
)
∵面SAB的法向量为
=(0,1,0)
∴cos<
,
>=
=
=
.
在正△SAB中,AB=2,SE=
| 3 |
| 3 |
∵BC=2,AD=1,E,F分别为AB,CD的中点,∴EF=
| 3 |
| 2 |
∵等边△SAB与直角梯形ABCD垂直,SE⊥AB
∴SE⊥面ABCD,∴SE⊥EF
直角△SEF中,|SF|=
| |SE|2+|EF|2 |
| ||
| 2 |
∴|
| SC |
| SD |
| SF| |
| 21 |
(2)建立如图所示的直角坐标系,

则S(0,0,
| 3 |
设面SCD的法向量为
| n2 |
|
|
取x=1,可得
| n2 |
| 3 |
∵面SAB的法向量为
| n1 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| 2 | ||
2
|
| ||
| 2 |
点评:本题考查面面垂直,考查线面垂直,考查向量知识的运用,考查面面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
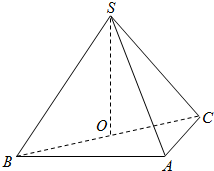 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.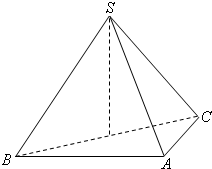 (2013•海口二模)如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
(2013•海口二模)如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.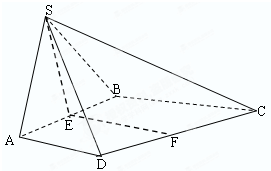 如图,等边△SAB与直角梯形ABCD垂直,AD⊥AB,BC⊥AB,AB=BC=2,AD=1.若E,F分别为AB,CD的中点.
如图,等边△SAB与直角梯形ABCD垂直,AD⊥AB,BC⊥AB,AB=BC=2,AD=1.若E,F分别为AB,CD的中点.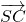
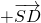 |的值;
|的值; 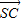
 |的值;
|的值;