Question

我们把平面直角坐标系中，函数y=f（x），x∈D上的点P（x，y），满足x∈N^*，y∈N^*的点称为函数y=f（x）的“正格点”．
（1）请你选取一个m的值，使对函数f（x）=sinmx，x∈R的图象上有正格点，并写出函数的一个正格点坐标
（2）若函数f（x）=sinmx，x∈R，m∈（1，2），与函数g（x）=lgx的图象有正格点交点，求m的值，并写出两个函数图象的所有交点个数．
（3）对于（2）中的m值，函数f（x）=sinx，x∈[0，]时，不等式log_ax＞sinmx恒成立，求实数a的取值范围．

Answer 1

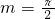解：（1）若取时，
正格点坐标（1，1），（5，1）（9，1）等（答案不唯一）…
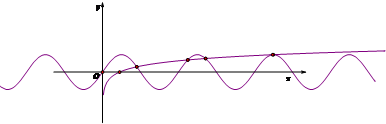
（2）作出两个函数图象，可知函数f（x）=sinmx，x∈R，与函数g（x）=lgx的图象有正格点交点只有一个点为（10，1）
∴，
∴．…
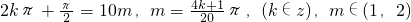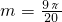根据图象可知：两个函数图象的所有交点个数为5个．（注意：最后两个点非常接近，几乎粘合在一起．）…
（3）由（2）知，
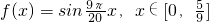∴①当a＞1时，不等式log_ax＞sinmx不能成立…
②当0＜a＜1时，由图（2）可知，∴…
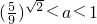分析：（1）取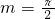，可求相应正格点坐标；
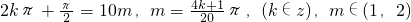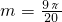（2）作出两个函数图象，利用图象可知正格点交点只有一个点为（10，1），从而有，所以，故可解；
（3）利用（2）的图象，分a＞1、0＜a＜1进行讨论．
点评：本题考查新定义，考查数形结合的思想，正确理解新定义时关键．