题目内容
甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸分别如下(单位:mm).
甲机床:10.2 10.1 10 9.8 9.9
10.3 9.7 10 9.9 10.1;
乙机床:10.3 10.4 9.6 9.9 10.1
10.9 8.9 9.7 10.2 10
(1)用茎叶图表示甲,乙两台机床所生产零件的尺寸;
(2)分别计算上面两个样本的平均数和方差.如果图纸规定零件的尺寸为10mm,从计算的结果来看哪台机床加工这种零件较合适?(要求写出公式,并利用公式笔算)
甲机床:10.2 10.1 10 9.8 9.9
10.3 9.7 10 9.9 10.1;
乙机床:10.3 10.4 9.6 9.9 10.1
10.9 8.9 9.7 10.2 10
(1)用茎叶图表示甲,乙两台机床所生产零件的尺寸;
(2)分别计算上面两个样本的平均数和方差.如果图纸规定零件的尺寸为10mm,从计算的结果来看哪台机床加工这种零件较合适?(要求写出公式,并利用公式笔算)
分析:(1)以整数部分为茎,小数部分为叶,分别表示表示甲,乙两台机床所生产零件的尺寸
(2)利用样本的平均数和方差公式计算得出样本的平均数和方差.并作出评判.
(2)利用样本的平均数和方差公式计算得出样本的平均数和方差.并作出评判.
解答: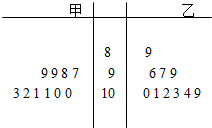 解:(1)如图所示,茎表示零件尺寸的整数环数,叶表示小数点后的数字.…(6分)
解:(1)如图所示,茎表示零件尺寸的整数环数,叶表示小数点后的数字.…(6分)
(2)
甲=
(x1+x2+…+xn)=
(10.2+10.1+…10.1)=
×100=10,…(7分)
乙=
(x1+x2+…+xn)=
(10.3+10.4+…+10)=
×10=10.…(8分)
=
[(x1-
甲)2+(x2-
甲)2+…+(xn-
甲)2]
∴=
[(10.2-10)2+(10.1-10)2+…(10.1-10)2]=0.03mm2
…(10分)
=
[(x1-
乙)2+(x2-
乙)2+…+(xn-
乙)2]
=
[(10.3-10)2+(10.4-10)2+…(10-10)2]=0.06mm2.…(12分)
∴
<
∵
甲=
乙而
<
∴用甲机床比乙机床稳定,即用甲机床加工较合适.…(14分)
 解:(1)如图所示,茎表示零件尺寸的整数环数,叶表示小数点后的数字.…(6分)
解:(1)如图所示,茎表示零件尺寸的整数环数,叶表示小数点后的数字.…(6分)(2)
. |
| x |
| 1 |
| n |
| 1 |
| 10 |
| 1 |
| 10 |
. |
| x |
| 1 |
| n |
| 1 |
| 10 |
| 1 |
| 10 |
| S | 2 甲 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
∴=
| 1 |
| 10 |
…(10分)
| S | 2 乙 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
=
| 1 |
| 10 |
∴
| s | 2 甲 |
| S | 2 乙 |
. |
| x |
. |
| x |
| s | 2 甲 |
| S | 2 乙 |
∴用甲机床比乙机床稳定,即用甲机床加工较合适.…(14分)
点评:方差是各变量值与其均值离差平方的平均数,它是测算数值型数据离散程度的最重要的方法.本题考查方差的定义与意义,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
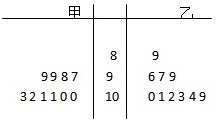 甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸用茎叶图表示如图,中间一列的数字表示零件尺寸的十位数(第三行是十位及百位,如甲,第三行对应零件尺寸为103,102,101,101…),两边的数字表示零件个数的个位数
甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸用茎叶图表示如图,中间一列的数字表示零件尺寸的十位数(第三行是十位及百位,如甲,第三行对应零件尺寸为103,102,101,101…),两边的数字表示零件个数的个位数