题目内容

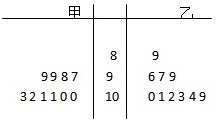甲、乙两台机床在相同的技术条件下，同时生产一种零件，现在从中抽测10个，它们的尺寸用茎叶图表示如图，中间一列的数字表示零件尺寸的十位数（第三行是十位及百位，如甲，第三行对应零件尺寸为103，102，101，101…），两边的数字表示零件个数的个位数
（1）分别计算这两个样本的平均数
（2）若规定零件的尺寸为10 0mm，从计算的结果来看哪台机床加工这种零件较合适？（要求写出公式，并利用公式笔算）
分析：（1）根据已知中茎叶图中数据，代入样本的平均数公式可得两个样本的平均数；
（2）根据茎叶图分析数据的离散程序，也可利用方差公式计算方差．并作出评判．
解答：解：（1）
.
甲
=
97+98+99+99+100+100+101+101+102+103
10
=100
.
乙
=
89+96+97+99+100+101+102+103+104+109
10
=100
故甲、乙平均数均为100
（2）从已知中茎叶图中数据，可知甲机床加工的零件的尺寸与10 0mm具有更好的集中性
故甲更合适
（也可代入方差公式，计算出S甲2=3，S乙2=
258
30
，利用方差小，离散程度越小，得到甲更合适）
点评：方差是各变量值与其均值离差平方的平均数，它是测算数值型数据离散程度的最重要的方法．本题考查方差的定义与意义，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
练习册系列答案
相关题目
甲、乙两台机床在相同的条件下同时生产一种零件，现在从中各抽测10个，它们的尺寸分别为（单位：mm）：
甲：10.2  10.1  10.9  8.9  9.9  10.3  9.7  10  9.9  10.1
乙：10.3  10.4  9.6  9.9  10.1  10  9.8  9.7  10.2  10
分别计算上面两个样本的平均数与方差，如果图纸上的设计尺寸为10 mm，从计算结果看，用哪台机床加工这种零件较合适？
甲、乙两台机床在相同的技术条件下，同时生产一种零件，现在从中抽测10个，它们的尺寸分别如下（单位：mm）．
甲机床：10.2        10.1        10           9.8          9.9
       10.3        9.7         10           9.9          10.1；
乙机床：10.3        10.4        9.6          9.9          10.1
       10.9        8.9         9.7          10.2         10
（1）用茎叶图表示甲，乙两台机床所生产零件的尺寸；
（2）分别计算上面两个样本的平均数和方差．如果图纸规定零件的尺寸为10mm，从计算的结果来看哪台机床加工这种零件较合适？（要求写出公式，并利用公式笔算）

甲、乙两台机床在相同的技术条件下，同时生产一种零件，现在从中抽测10个，它们的尺寸分别如下（单位：mm）.

甲机床：10.2  10.1  10  9.8  9.9  10.3  9.7  10  9.9  10.1；

乙机床：10.3  10.4  9.6  9.9  10.1  10.9  8.9  9.7  10.2  10.

分别计算上面两个样本的平均数和方差.如图纸规定零件的尺寸为10 mm，从计算的结果来看哪台机床加工这种零件较合适？
甲、乙两台机床在相同的条件下同时生产一种零件,现在从中各抽测10个,它们的尺寸分别为(单位:mm):

甲:10.2  10.1  10.9  8.9  9.910.3  9.7  10   9.9   10.1

乙:10.3  10.4  9.6   9.9  10.110   9.8  9.7  10.2  10

分别计算上面两个样本的平均数与标准差.如果图纸上的设计尺寸为10 mm,从计算结果看,用哪台机床加工这种零件较合适.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网