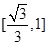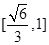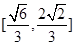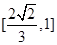题目内容
(本小题满分13分)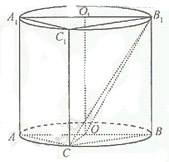
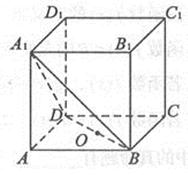
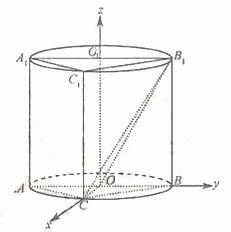
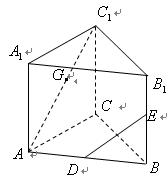
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,
三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径。
(Ⅰ)证明:平面A1ACC1⊥平面B1BCC1;
(Ⅱ)设AB=AA1。在圆柱OO1内随机选取一点,记该点取自于
三棱柱ABC-A1B1C1内的概率为P。
(i) 当点C在圆周上运动时,求P的最大值;
记平面A1ACC1与平面B1OC所成的角为 (0°<
(0°< 
 90°)。当P取最大值时,求cos
90°)。当P取最大值时,求cos 的值。
的值。
本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,以及几何体的体积几何概型等基础知识;考查空间想象能力、推理论证能力、运算求解能力;考查数形结合思想、化归与转化思想、必然与或然思想。满分13分。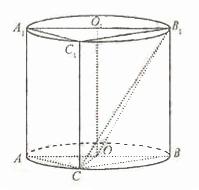
解法一 :
(I)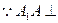 平面
平面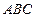 ,
,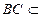 平面
平面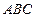 ,
, 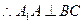
 是圆O的直径,
是圆O的直径, 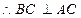
又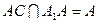 ,
, 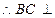 平面
平面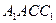
而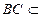 平面
平面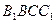 ,
,
所以平面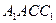
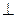 平面
平面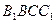 。
。
(II)(i)设圆柱的底面半径为r,则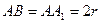
故三棱柱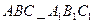 的体积
的体积
又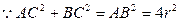
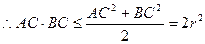
当且仅当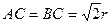 时等号成立。
时等号成立。
从而,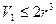
而圆柱的体积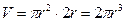 ,
,
故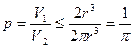 ,当且仅当
,当且仅当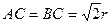 ,即
,即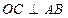 时等号成立。
时等号成立。
所以,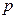 的最大值等于
的最大值等于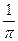
(ii)由(i)可知,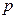 取最大值时,
取最大值时,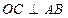
于是,以O为坐标原点,建立空间直角坐标系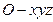 (如图),
(如图),
则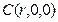 ,
,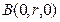 ,
,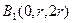
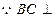 平面
平面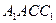 ,
,
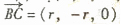 是平面
是平面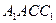 的一个法向量
的一个法向量
设平面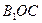 的法向量
的法向量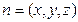 ,
,
取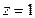 ,得平面
,得平面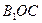 的一个法向量为
的一个法向量为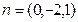
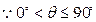 ,
, 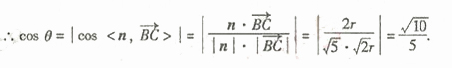
解法二:
(I)同解法一
(II)(i)设圆柱的底面半径为r,则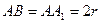 ,
,
故三棱柱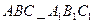 的体积
的体积

设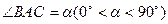 ,
,
则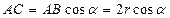 ,
,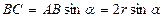 ,
,
由于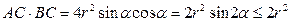 ,当且仅当
,当且仅当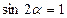 即
即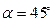 时等号成立,故
时等号成立,故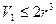
而圆柱的体积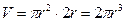 ,
,
故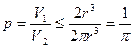 ,当且仅当
,当且仅当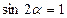 即
即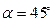 时等号成立。
时等号成立。
所以,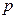 的最大值等于
的最大值等于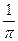
(ii)同解法一
解法三:
(I)同解法一
(II)(i)设圆柱的底面半径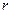 ,则
,则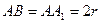 ,故圆柱的体积
,故圆柱的体积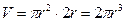
解析

练习册系列答案
相关题目
已知两条不同的直线m、n,两个不同的平面a、β,则下列命题中的真命题是( )
| A.若m⊥a,n⊥β,a⊥β,则m⊥n | B.若m⊥a,n∥β,a⊥β,则m⊥n |
| C.若m∥a,n∥β,a∥β,则m∥n | D.若m∥a,n⊥β,a⊥β,则m∥n |
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,则能得出
是两个不同的平面,则能得出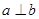 的是( )
的是( )
A.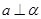 , ,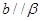 , ,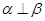 | B.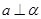 , ,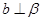 , ,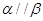 |
C.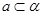 , ,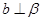 , ,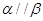 | D.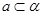 , ,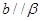 , ,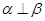 |

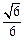 ,求四棱锥P-ABCD的体积.
,求四棱锥P-ABCD的体积.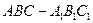 中,
中,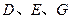 分别是
分别是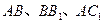 的中点,
的中点, .
.
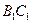 上是否存在点
上是否存在点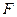 使
使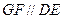 ?如果存在,试确定它的位置;如果不存在,请说明理由;
?如果存在,试确定它的位置;如果不存在,请说明理由;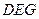 与底面
与底面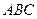 所成锐二面角的正切值;
所成锐二面角的正切值;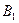 到截面
到截面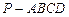 中,底面
中,底面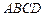 是一直角梯形,
是一直角梯形,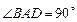 ,
,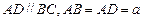 ,
,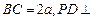 底面
底面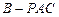 的体积;
的体积;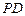 上是否存在一点
上是否存在一点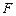 ,使得
,使得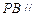 平面
平面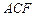 ,若存在,求出
,若存在,求出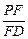 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.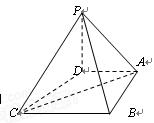
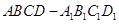 中,点
中,点 为线段
为线段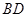 的中点.设点
的中点.设点 在线段
在线段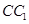 上,直线
上,直线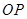 与平面
与平面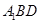 所成的角为
所成的角为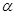 ,则
,则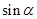 的取值范围是( )
的取值范围是( )