题目内容
已知矩形ABCD的边AB=a，BC=2，PA⊥平面ABCD，PA=2，现有以下五个数据：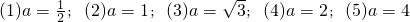
，
当在BC边上存在点Q，使PQ⊥QD时，则a可以取________．（填上一个正确的数据序号即可）
①或②
分析：根据三垂线定理结合PQ⊥QD，可得PQ在底面的射影AQ也与QD垂直，由此可得平面ABCD内满足条件的Q点应在以AD为直径的圆上，得出a≤1即可选出正确选项．
解答：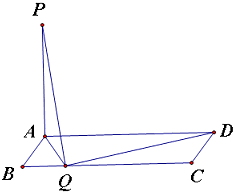
解：连接AQ，
因为PQ⊥QD，根据三垂线定理可得AQ⊥QD
在平面ABCD内，直径所对的圆周角为直角
所以Q点在以AD为直径的圆上，
故当BC与以AD为直径的圆有公共点时，在BC边上存在点Q，使PQ⊥QD
因此AB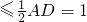
，即a≤1
故答案为：①或②
点评：本题考查了空间的直线与平面、直线与直线的位置关系，属于中档题．充分利用三垂线定理和平面内点的轨迹，是解决本题的关键所在．
分析：根据三垂线定理结合PQ⊥QD，可得PQ在底面的射影AQ也与QD垂直，由此可得平面ABCD内满足条件的Q点应在以AD为直径的圆上，得出a≤1即可选出正确选项．
解答：
解：连接AQ，因为PQ⊥QD，根据三垂线定理可得AQ⊥QD
在平面ABCD内，直径所对的圆周角为直角
所以Q点在以AD为直径的圆上，
故当BC与以AD为直径的圆有公共点时，在BC边上存在点Q，使PQ⊥QD
因此AB
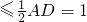，即a≤1故答案为：①或②
点评：本题考查了空间的直线与平面、直线与直线的位置关系，属于中档题．充分利用三垂线定理和平面内点的轨迹，是解决本题的关键所在．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
已知矩形ABCD的边AB=4cm，BC=3cm，如图所示，矩形的顶点A，B为某一椭圆的两个焦点，且椭圆经过矩形的另外两个顶点C，D，试建立适当的坐标系，求椭圆的方程．