Question

已知矩形ABCD的边长为2，点P在线段BD上运动，则

AP

•

AC

=

4

．

Answer 1

分析：设AC∩BD=O，由题可知|

AO

|=

1

2

|

AC

|=

2

，再根据要求的式子为|

AP

|•|

AC

|•cos∠PAO=2|

AO

|² ，
从而求得结果．

解答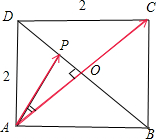：解：设AC∩BD=O，由题可知AC⊥BD，AC、BD被点O平分，
|

AO

|=

1

2

|

AC

|=

2

，
则

AP

•

AC

=|

AP

|•|

AC

|•cos∠PAO=|

AP

|（2|

AO

|）cos∠PAO
=2|

AO

|²=4，
故答案为 4．

点评：本题主要考查两个向量的数量积的定义，两个向量的加减法及其几何意义，属于中档题．