题目内容
已知矩形ABCD的边AB=1，BC=a，PA⊥平面ABCD，问BC边上是否存在点Q，使得PQ⊥QD？并说明理由．
分析：PA⊥平面ABCD，PQ⊥QD可得QD⊥AQ，可得△ABQ∽△QCD，可求a的范围．
解答：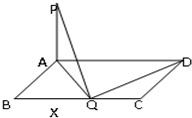
解：假设在BC边上存在点Q，使得PQ⊥QD，（2分）
因为PA⊥平面ABCD，所以PA⊥QD，又由于PQ⊥QD，
所以QD⊥平面APQ，则QD⊥AQ，即∠AQD=90°，
易得△ABQ∽△QCD，设BQ=X，所以有X（a-X）=1
即：x2-ax+1=0
所以当△=a2-4≥0时，上方程有解，（8分）
因此，当a≥2时，存在符合条件的点Q，否则不存在．（10分）
解：假设在BC边上存在点Q，使得PQ⊥QD，（2分）因为PA⊥平面ABCD，所以PA⊥QD，又由于PQ⊥QD，
所以QD⊥平面APQ，则QD⊥AQ，即∠AQD=90°，
易得△ABQ∽△QCD，设BQ=X，所以有X（a-X）=1
即：x2-ax+1=0
所以当△=a2-4≥0时，上方程有解，（8分）
因此，当a≥2时，存在符合条件的点Q，否则不存在．（10分）
点评：这是一道探究题，此类问题的解决方法有两种，一是先找后证，二是直接推出．本题用的是第二种方法．
练习册系列答案
相关题目
已知矩形ABCD的边AB=4cm，BC=3cm，如图所示，矩形的顶点A，B为某一椭圆的两个焦点，且椭圆经过矩形的另外两个顶点C，D，试建立适当的坐标系，求椭圆的方程．